马尔可夫决策过程¶
约 555 个字 2 张图片 预计阅读时间 3 分钟
随机过程:一列随时间变化的随机变量,当时间是离散量时,一个随机过程可以表示为\(\set{X_t}_{t=0,1,\cdots}\),每个\(X_t\)都是一个随机变量
马尔可夫性:下一时刻的状态\(X_{t+1}\)只由当前状态\(X_t\)决定
\[
P(X_{t+1}=x_{t+1}|X_0=x_0,X_1=x_1,\cdots,X_t=x_t)=P(X_{t+1}=x_{t+1}|X_t=x_t)
\]
状态转移概率:\(P(S_{t+1}|S_t)\)
奖励函数:\(R_{t+1}:=R(S_t,S_{t+1})\),从第t步转移到第t+1步获得的奖励
回报:反应该时刻得到的累加奖励 $$ G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdots $$
折扣因子\(\gamma\in[0,1]\),\(R_{t+k}\)表示第\(t+k\)时刻获得的奖励
马尔可夫决策过程:\(MDP=(S,A,P,R,\gamma)\)
- 状态集合\(S\):求解问题中所有可能出现的状态构成的集合,这个集合可能是一个有限的集合,也可能是一个无限的集合
- 动作集合\(A\):求解问题中智能体能够采取的所有动作构成的集合,这个集合同样可以是有限的,也可以是无限的
- 状态转移概率\(P(S_{t+1}|S_t,A_t)\):表示在当前状态\(S_t\)下采取动作\(A_t\)后进入下一时刻状态\(S_{t+1}\)的概率。显然,状态转移概率满足马尔可夫性。状态转移可以是概率性的(stochastic),也可以是确定的(deterministic)。确定的状态转移指在给定状态\(S_t\)下采取动作\(A_t\)后,转移到某一状态的概率为1
- 奖励函数\(R(S_t,A_t,S_{t+1})\):在状态\(S_t\)下执行动作\(A_t\)后到达状态\(S_{t+1}\)时,智能体能够得到的奖励
- 折扣因子\(\gamma\):后续时刻奖励对当前动作的价值系数,\(\gamma\in[0,1]\)

交互:
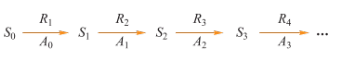
- 轨迹:状态序列\((S_0,S_1,\cdots)\)
- 状态序列中包含终止状态的问题叫作分段问题,不包含终止状态的问题叫作持续问题;在分段问题中,一个从初始状态到终止状态的完整轨迹称为一个片段