技术实现和逻辑设计 | Implementation Technology and Logic Design¶

约 2545 个字预计阅读时间 13 分钟

表示逻辑的方法

真值表(Truth Table)；
布尔函数(Boolean Function)；
卡诺图(Karnaugh Maps)；
时序图(Timing Diagram)；
逻辑电路图(Logic Circuit)；

其中，下划线的方法在功能确定的情况下，其表示是唯一的。

而我们的设计，就是在满足功能的前提下，尽可能优化和找到最好的设计。

而主要的设计过程如下：

确定系统的行为；
阐述输入和输出之间的逻辑关系，并用真值表或逻辑表达式表达出来；
优化逻辑表达以减少成本(比如使用卡诺图)；
将优化后的逻辑设计工艺映射到硬件实现上；
验证正确性（在仿真环境中）；


graph LR;

A["实际问题"] ===> B["真值表"]

B ==>|"化简"| C["最简功能"] ===>|"工艺映射"| D["网表"]

B ==>|"变换"| E["合适的表达式"] ===>|"工艺映射"| D

分层设计 | Hierarchical Design¶

分层设计即将复杂问题模块化分解为若干层次，然后逐个抽象解决。

其设计方法分为 自顶向下(Top-Down) 和 自底向上(Bottom-Up)。

前者从需求开始，自顶向下分解功能设计；后者根据现有的元件去组合成目标功能。

集成电路 | Integrated Circuit¶

集成电路 又叫 芯片(chip)，分为如下若干等级：

SSI(small-scale integrated) 含不到 10 个 gates；
MSI(medium-scale integrated) 含 10 ~ 100 个 gates；
LSI(large-scale integrated) 含成百上千个 gates；
VLSI(very large-scale integrated) 含成千上亿个 gates；

技术参数¶

门的实现主要通过这些参数特性来描述：

Name	Description
Fan-in	一个逻辑门可用的输入数量
Fan-out	一个逻辑门输出时可驱动的标准负载数量
Logic Levels	高低电平的输入输出电压范围
Noise Margin	对外界噪声的容忍能力(具体来说是不会导致行为异变的最大噪声阈值)
Cost for a gate	衡量门对集成电路成本的贡献
Propagation Delay	输入信号改变后，输出改变所需的时间
Power Dissipation	电源输出能耗和门的能耗

扇入\扇出 | Fan-in\out¶

扇入描述了一个门能够接受的最多输入量，如一个四输入与非门的扇入就是 4；

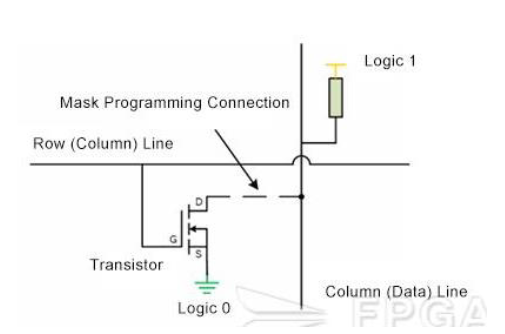
Alt text

而扇出描述的则是一个门的输出(栅极输出)在不降低工作性能的情况下能够负载多少门，例如一个非门的输出能够同时负载 4 个非门并且都能正常工作，则其扇出为 4，其也能通过标准负载来定义。

Alt text

标准负载

所谓的标准负载，是衡量“负载”的一个“单位砝码”。其大小等于一个非门(逆变器)贡献的负载压力。

那么要如何评估负载呢？首先我们引入 转换时间(transition time)：

转换时间 | Transition Time¶

转换时间分为 \(\mathrm{t_{LH}}\)(rise time) 和 \(\mathrm{t_{HL}}\)(fall time) 两个部分。

rise time 等于栅极输出从 \(\mathrm{V_{CC}}\) 的 10% 升高到 90% 所需要的时间；
fall time 等于栅极输出从 \(\mathrm{V_{CC}}\) 的 90% 降低到 10% 所需要的时间；

通过时序图表示就是这样：

随着负载增加，转换时间也会增加（给电容充电的时间增加），而扇出定义中提到的“最大负载”，就是指它的转换时间不超过它预定的最大转换时间。

从左到右表示负载不断增加时，rise time 的变化趋势。

传播延迟¶

传播延迟(propagation delay) 衡量了门的输入变化导致输出变化所需要的时间。由于从低电平转化到高电平和高电平转化到低电平所需要的时间不一样，所以传播延迟同样有两个部分，分别使用 \(\mathrm{t_{PHL}}\) 和 \(\mathrm{t_{PLH}} 来表示\)。

更具体的来说，传播延迟的计算方法是输入和输出的变化中点（即变化到 \(\frac{1}{2}V_{CC}\) 时）的时间差，通过时序图表示就是这样：

此外，我们还可以引入 \(\mathrm{ t_{pd} }\) 来统一表示 \(\mathrm{t_{PHL}}\) 和 \(\mathrm{t_{PLH}}\)。数值上，\(\mathrm{ t_{pd} } = average(\mathrm{t_{PHL}}, \mathrm{t_{PLH}})\) 或 \(\mathrm{ t_{pd} } = max(\mathrm{t_{PHL}}, \mathrm{t_{PLH}})\)。

题面答案

根据时序图，写出门的传播延迟，此处 \(\mathrm{ t_{pd} } = average(\mathrm{t_{PHL}}, \mathrm{t_{PLH}})\)。