跳转至

组合功能模块 | Combinational Functional Blocks

约 2218 个字 预计阅读时间 11 分钟

基本逻辑函数

  • 常量函数(Value-Fixing)：\(F=0\;\;or\;\;F=1\) | 输出定值；
  • 传输函数(Transferring)：\(F=X\) | 直接输出输入值；
  • 逆变函数(Inverting)：\(F=\overline{X}\) | 输出输入的相反；

  • 使能函数(Enabling)：\(F=X\cdot En \;\; or \;\; F = X + \overline{En}\) | 通过使能控制输出是否可变，分为两种，比如与的形式中，只有 \(En\) 为 1 时，\(F\) 表现为 \(X\) 的值；反之输出必定为 0（注意区分它与三态门的区别，高阻态or定值）；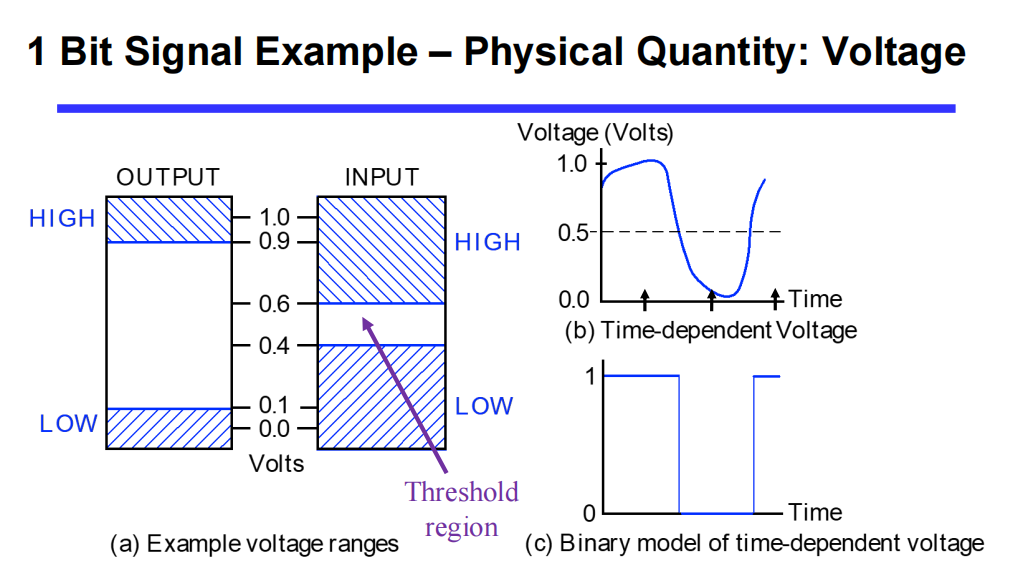

    Alt text

  • 多位基本函数(Multiple-bit Rudimentary Functions): 传输过程中用总线(bus)表示

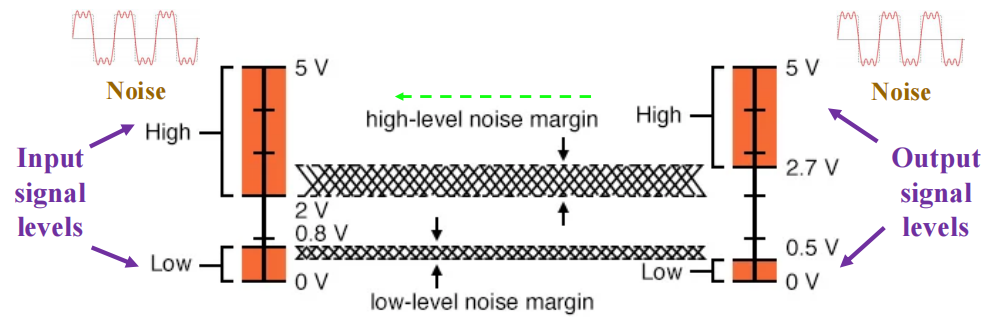
    Alt text

基本功能块 | Functional Blocks

最广泛，最有用的四个功能块

  • 译码器(Decoder)

  • 编码器(Encoder)

  • （三端）多路选择器(Multiplexer) MUX

  • （三端）信号分离器(Demultiplexer) DEMUX

Alt text

译码器 | Decoder

译码器（Decoder）能将信息从 \(n\) 个输入转换为 \(2^n\) 个或更少的唯一输出。具体是怎么实现的呢？实际上，译码器是在枚举 \(n\) 个输入的所有排列方式（共 \(2^n\) 种）。更进一步的，这可以理解为是在枚举最小项（minterms）。比如 \(3-to-8\) 译码器，当输入为某个特定组合 101 时，只有相应的表示 101（或者说 \(\sum_m(5)\)）这个组合的输出是 1。

如何构造一个 \(n-to-2^n\) 译码器？我们用递归的思路来求解：

  1. 设 \(k=n\)；
  2. 如果 \(k\) 为偶数，问题分解为设计两个 \(\frac{k}{2}-to-2^{\frac{k}{2}}\) 译码器，并将它们用 \(2^k\) 个与门连接起来；如果 \(k\) 为奇数，问题分解为设计一个 \(\frac{k-1}{2}-to-2^{\frac{k-1}{2}}\) 和一个 \(\frac{k+1}{2}-to-2^{\frac{k+1}{2}}\) 译码器，并将它们用 \(2^k\) 个与门连接起来；
  3. 对每个译码器重复第二步，直到 \(k=1\)，这时候我们使用一个 \(1-to-2\) 译码器；

\(3-to-8\)

设计一个 \(3-to-8\) 译码器。

  1. \(k=3\)，为奇数，分解为 \(2-to-4\) 和 \(1-to-2\) 译码器，并将它们用 \(2^3\) 个与门连接起来；
  2. \(k=2\)，为偶数，分解为两个 \(1-to-2\) 译码器，并将它们用 \(2^2\) 个与门连接起来；
  3. \(k=1\)，使用一个 \(1-to-2\) 译码器；

Alt text

通过上图可以看到，用门连接的方式就是下方与上方的笛卡尔积：比如上方输出为\((B, C, D, E)\)，下方输出为\((\overline{A}, A)\)，则 链接方式为\((B, \overline{A}), (C, \overline{A}), (D, \overline{A}), (E, \overline{A}), (B, A), (C, A), (D, A), (E, A)\)

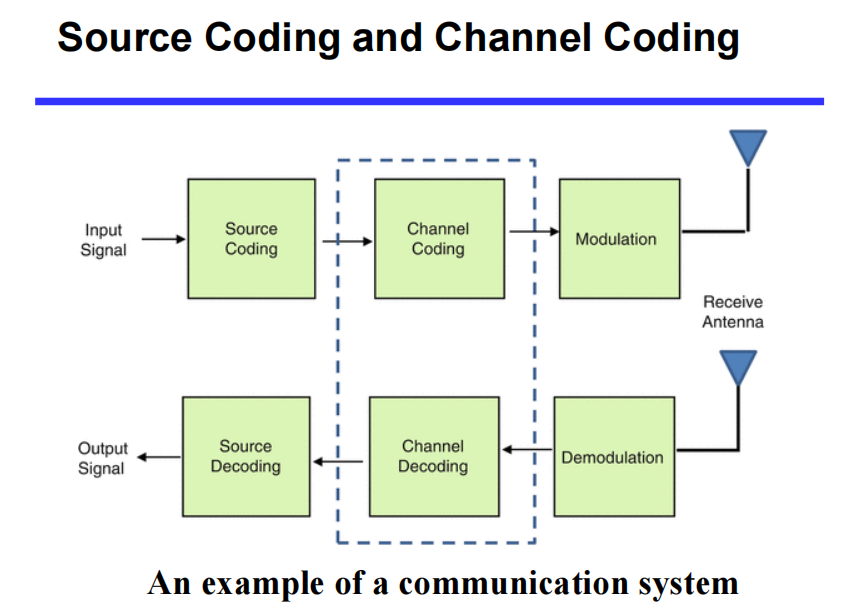
Alt text

\(6-to-64\)

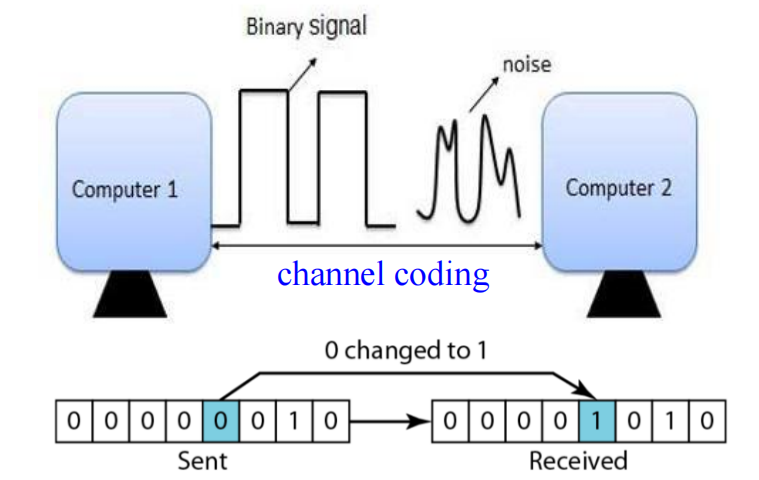
Alt text

原先的门输入代价为 \(GN = 6+6*64=390\)

用译码器分层实现后，门输入代价为 \(GN = 6 + 2*64 + 2*2*8 + 2*2*4 = 182\)

\(8-to-256\)

Alt text

添加使能端

我们通常会为译码器添加一个使能端：

Alt text

事实上，这也可以称作信号分离器(demultiplexer)

运用使能端的\(3-8\)译码器

Alt text

轮流使能。空间比刚刚的二分法大了。

译码器的应用

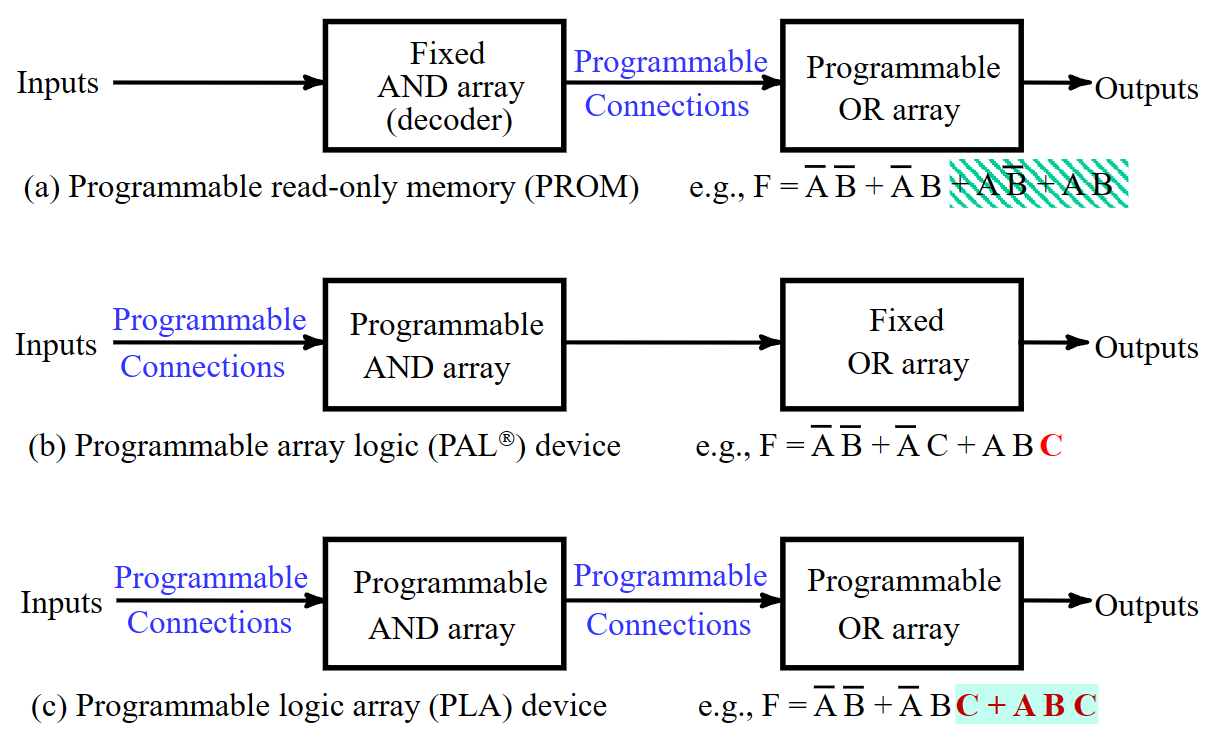
译码器本质上完成了枚举最小项的工作，如果我们在译码器的输出后面接上或门，就可以实现 SOM 的逻辑表达。因为 SOM 可以表达任何组合逻辑，所以译码器就可以实现任何的组合逻辑。

由于底层的电路能够直接实现的运算十分局限，所以需要用译码器来实现一些基础运算，例如加法。

一位加法器就可以通过译码器和或门实现，核心就是枚举输入的各种情况，然后用或门拾取 sum 和 carry 的最小项。

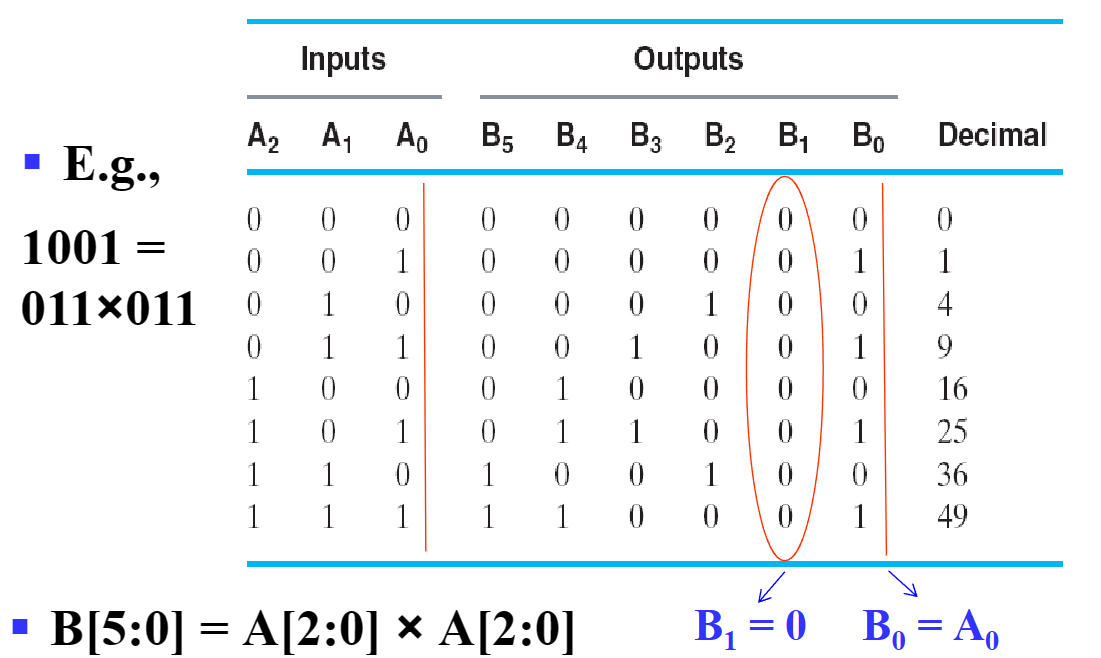
Alt text

首先要判断使用的数码管是共阳极(Common anode)还是共阴极(Common cathode)，这会导致发光的有效电平不同

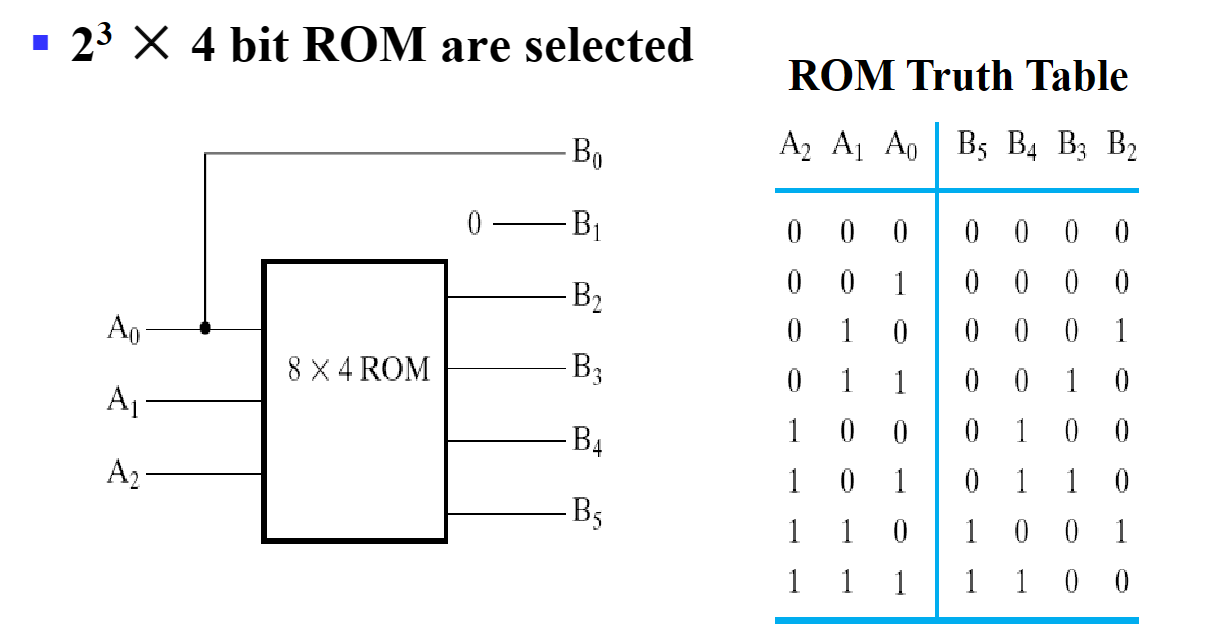
Alt text

之后就可以通过真值表来进行设计(此时是共阴极)

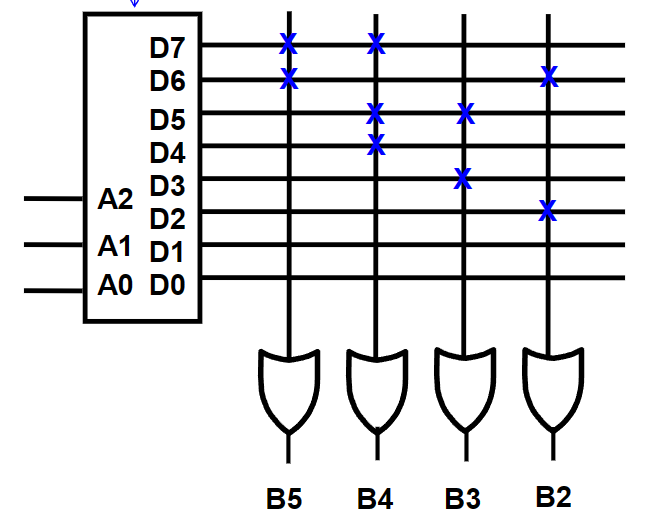
Alt text

编码器 | Encoder

编码器（Encoder）与译码器是对称的，能将信息从 \(2^n\) 个或更少的输入转换为 \(n\) 个输出。但和译码器不同的是，普通编码器必须要求输入是 one-hot 的，即只允许存在一个输入为 1，否则无法判断得出唯一输出。此外，编码器的逻辑表达式和具体电路实现，通常都比译码器更为复杂。

one hot -> binary

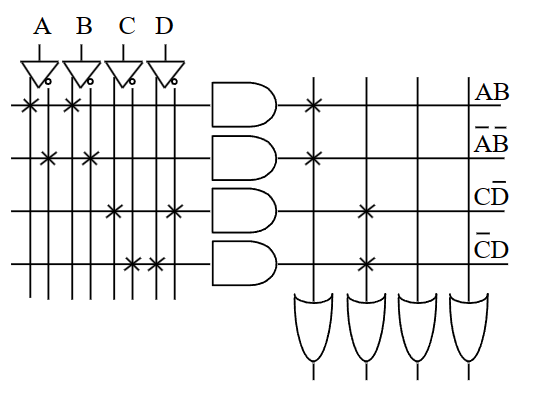
Alt text

使用独热码的时候，因为别的输入都是未知的，如果别的量作X来方便优化，那此时就无法判断得出唯一输出。

优先编码器

优先编码器（Priority Encoder）可以解决上述问题。

优先编码器能够实现优先级函数，它不要求输入是 one-hot 的，而是总是关注有效输入中优先级最高的那一个。即比如当优先级最高的那一位是 1 时，其它所有优先级不如它的位置的值都是我们不关心的内容了。

中断(interrupt)判优器

优先编码器的一种应用就是中断判优器。

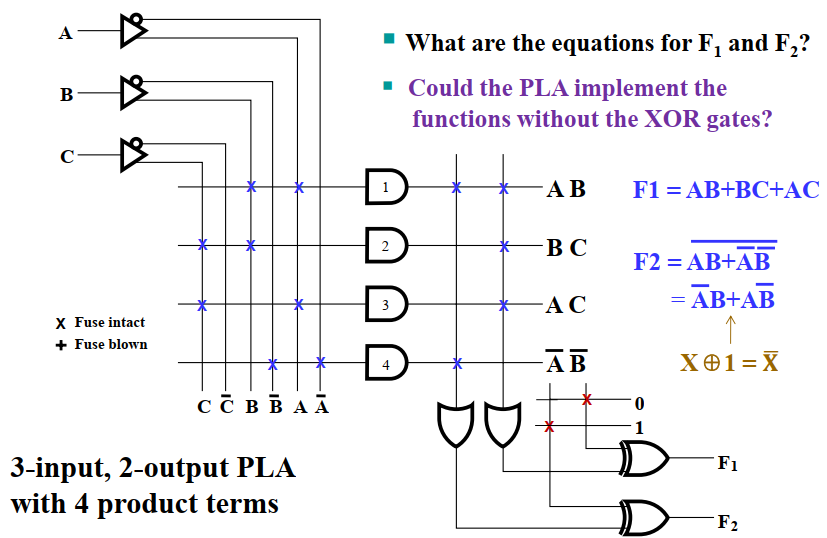
Alt text

其中 \(V\) 表示输出是否有效，在中断判优系统中即表示是否有中断请求。

计算逻辑表达式

是正难求反的思路。

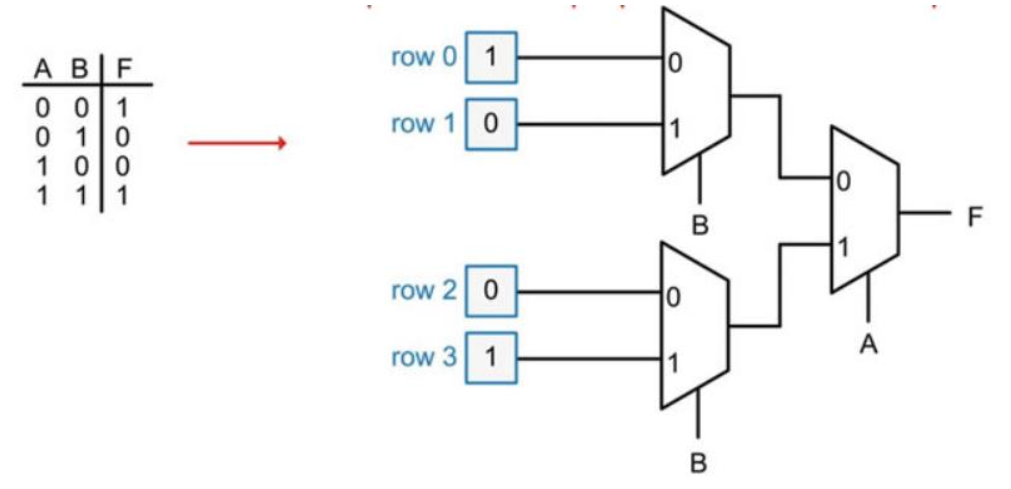
Alt text

Alt text

多路选择器 | Multiplexer

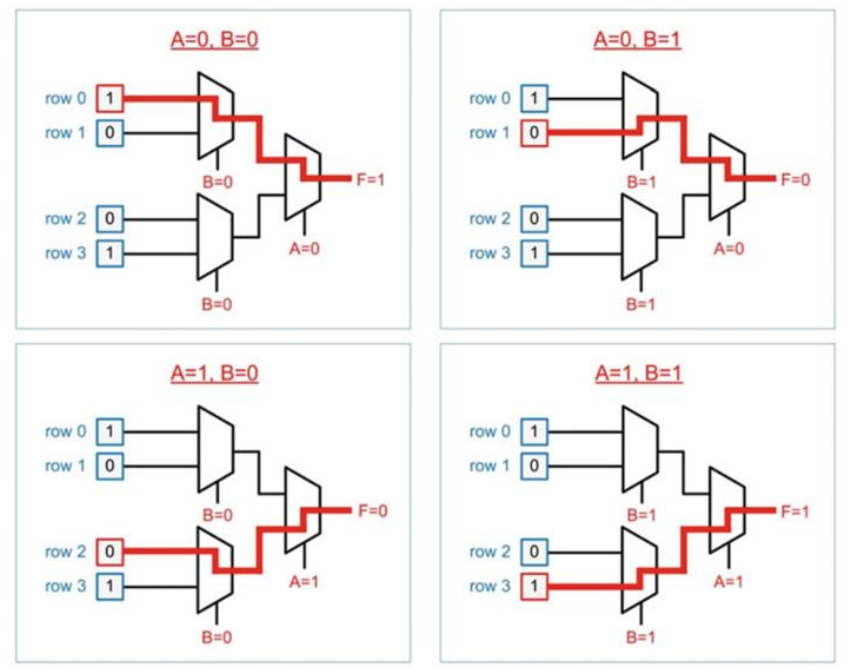
多路复用器（Multiplexer，或称为数据选择器）可以通过 \(n\) 个控制信号，对 \(2^n\) 个或更少的数据信号做选择，并得到 \(1\) 个选择结果输出。

MUX 和译码器一样，都可以表达任意组合逻辑。这是因为 MUX 的实现内部就存在一个译码器，我们只需要将 MUX 的控制端（也就是译码器）用作输入，将组合逻辑的真值表写入 MUX 的选项端进行选择，就可以表达任何组合逻辑。

通常，一个 \(2^n-to-1\) MUX 的组成为：

  • 一个 \(n-to-2^n\) 译码器（MUX 利用了译码器每次只有一个输出为 1 的特性，从而实现选择功能）；
  • \(2^n \times 2\) AND-OR；

a

Alt text

如果使用三态门来实现 MUX，那么门输入将大大减少。

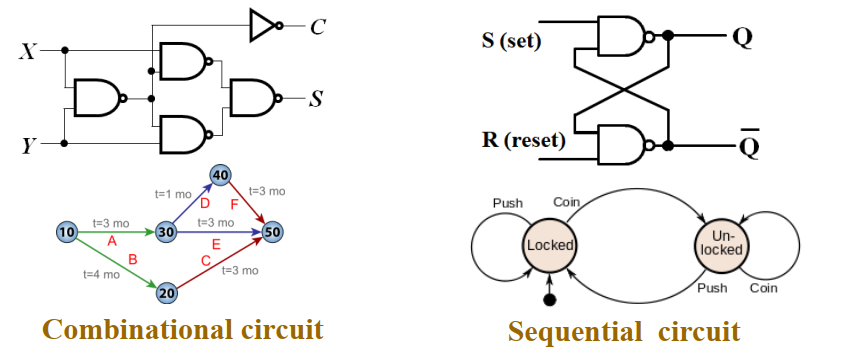
Alt text

Alt text

完全使用三态门来实现四输入 MUX，门输入大大减少。

重要：MUX 还可以 实现任意的逻辑函数：

  • 将控制端当作输入，原来的输入当作待选择的值；
  • 即可以将一个四输入 MUX 当作一个二输入的函数；

换句话来说，就是将原来的控制端当作输入端，并在原来的输入端写入逻辑函数的真值表，以实现任意逻辑函数。

Gray To Binary

Gray To Binary 的真值表为

Gray
A B C		 Binary
X Y Z
000 000
001 111
010 011
011 100
100 001
101 110
110 010
111 101

我们就可以用一个三输入 MUX （以控制端作为输入，原输入端为常量）来实现这个函数：

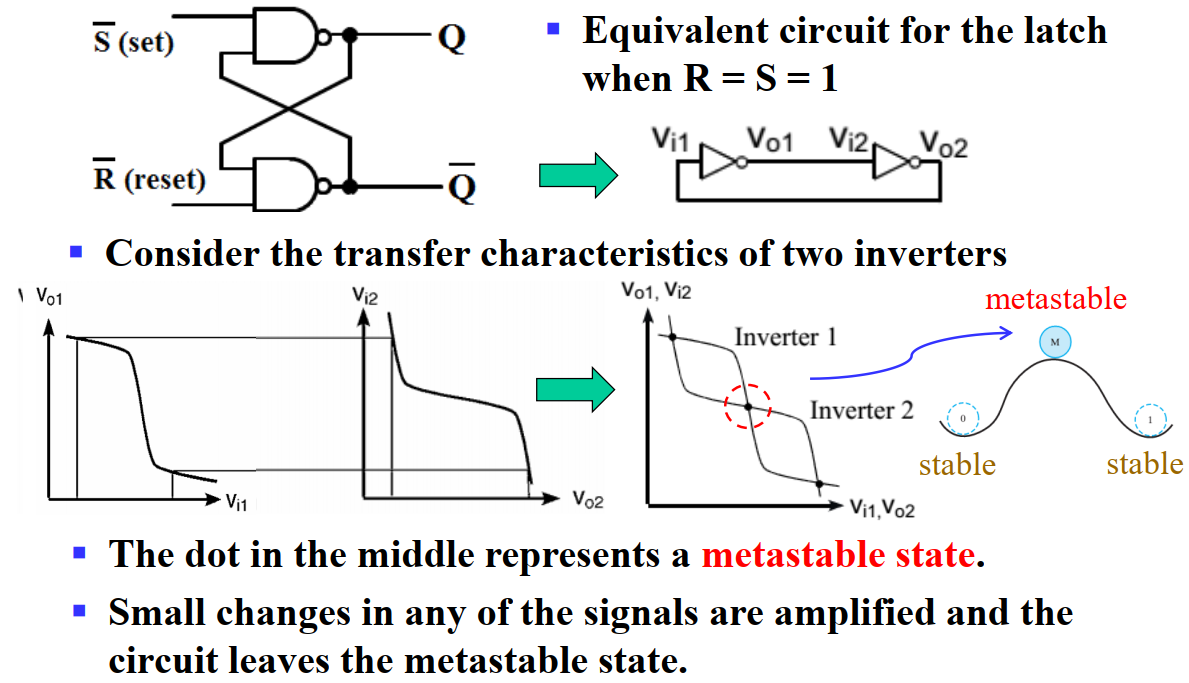
Alt text

我们还可以通过把一部分的输入当作常量端来简化元件（降维）：

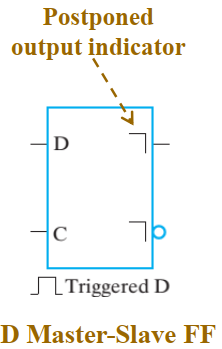
Alt text

观察其最小项，使其输出所有最小项。

实际上在降维过程中并不需要全都是 C，如果卡诺图中存在双 1 或者双 0，也可以仍然使用常量。

译码器与多路复用器

译码器和多路复用器的原理与实现都有相似之处。如果我们要实现任何组合逻辑，大部分情况下使用译码器会更好，因为它只需要把枚举出的最小项用一个或门连接即可，而 MUX 则需要用很多的与门来达到相同的效果。当然，在某些情况下 MUX 可以进行降维优化，有时候会比译码器效果更好。

事实上，这样的比较不算公平，因为它们虽然很相似，但设计的目的是差别很大的。译码器用于译码（interpret a coded data），而 MUX 用于选择并传输数据（select and transmit data）。虽然 MUX 中经常用译码器来作为控制端，但 MUX 中的译码器和一个正常的译码器的用途相去甚远：MUX 中的译码器只用于控制，它用 \(n\) 个输入信号来表示选择 \(n\) 个待选项中的哪一项，译码器信号本身并不传递除了“选择”之外的任何意义；而在一个正常的译码器中，\(n\) 个输入显然是有意义的，它们就是译码器所“译”的“码”。这就是两者的区别。

题目例子

Alt text

\(O_0\)=\(\overline{A}\overline{B}\)，\(O_1\)=\(\overline{A}B\)，\(O_2\)=\(A\overline{B}\)，\(O_3\)=\(AB\)

\(O\) \(CD\)
\(O_0\) 00
\(O_1\) 01
\(O_2\) 10
\(O_3\) 11

\(\therefore F = O_0\overline{C}\overline{D} + O_1\overline{C}D + O_2C\overline{D} + O_3CD=\overline{A}\overline{B}\overline{C}\overline{D} + \overline{A}B\overline{C}D + A\overline{B}C\overline{D} + ABCD\)

信号分离器 | Demultiplexer

简写为 DEMUX，通过控制端选择输入给到若干输出中的哪一个。

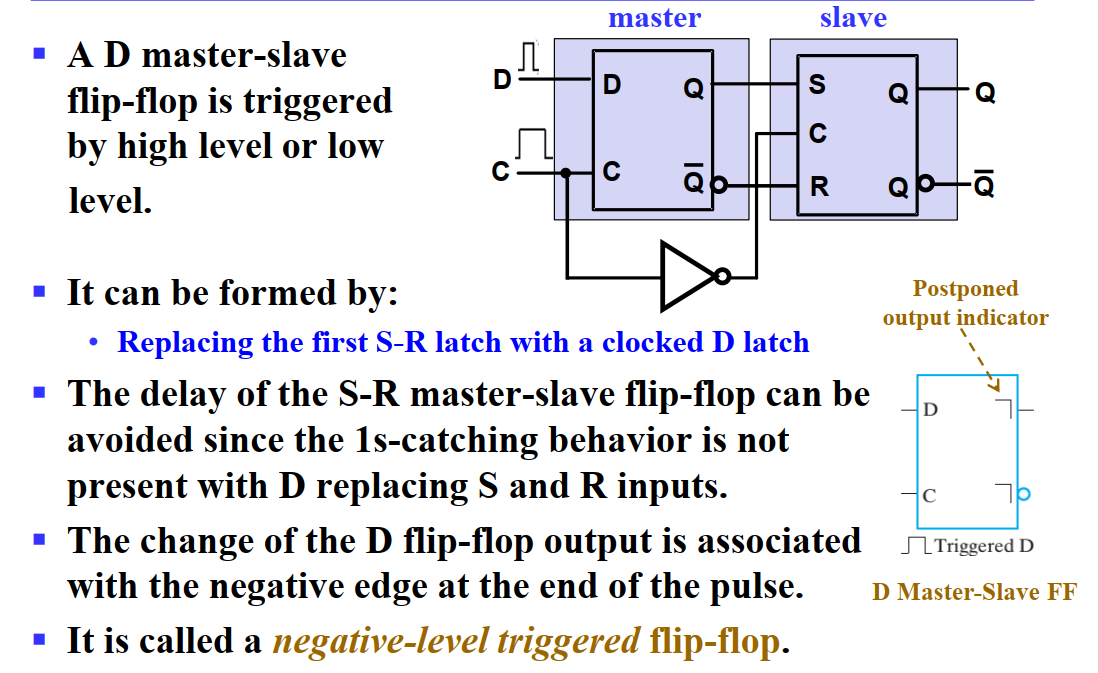
Alt text

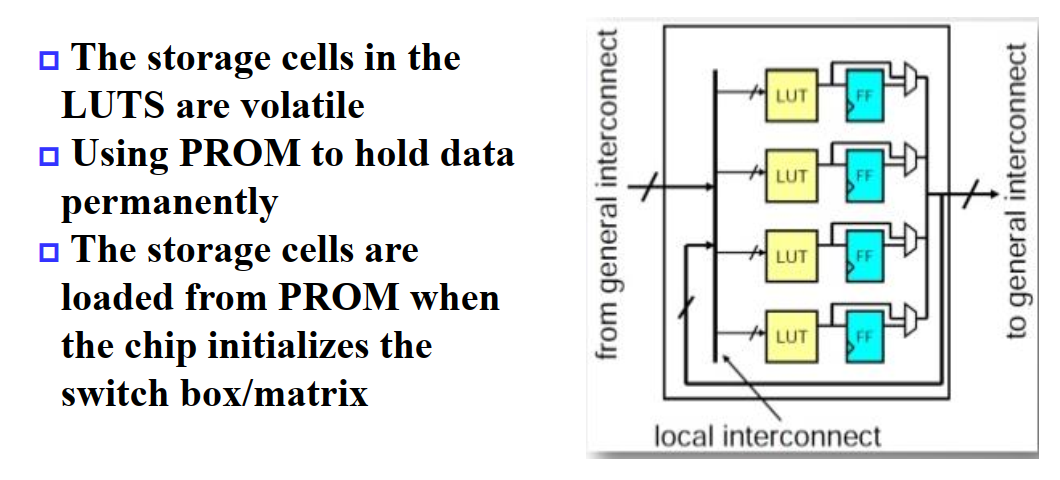
后续 👉 可编程技术