存储元件与时序电路分析¶
约 3753 个字 23 张图片 预计阅读时间 19 分钟
引入
时序电路中最重要的就是信息存储元件。当输入信号不发生变化时(重点是变化,即输入和存储信息未必存在对应关系)存储元件就能够保持其内部存储的二进制数据。
存储元件主要有 锁存器(latch) 和 触发器(flip-flop) 两种,其中前者是后者的基础,或者说多数情况下我们使用后者,但后者由前者构成。
锁存器 | Latch¶
缓冲
缓冲器(buffer) 一般通过两个非门串联,并将输入连通输出实现,这样能够实现信息的存储,然而无法修改。而锁存器就是在缓冲器的基础上,将非门替换为或非门或与非门实现的。

其中,从给定输入到更新输出有一个 \(t_G\) 的延时。
Metastable
在 (d) 图中,可能会产生 亚稳态(metastable)。这在 Latch 中也可能出现。
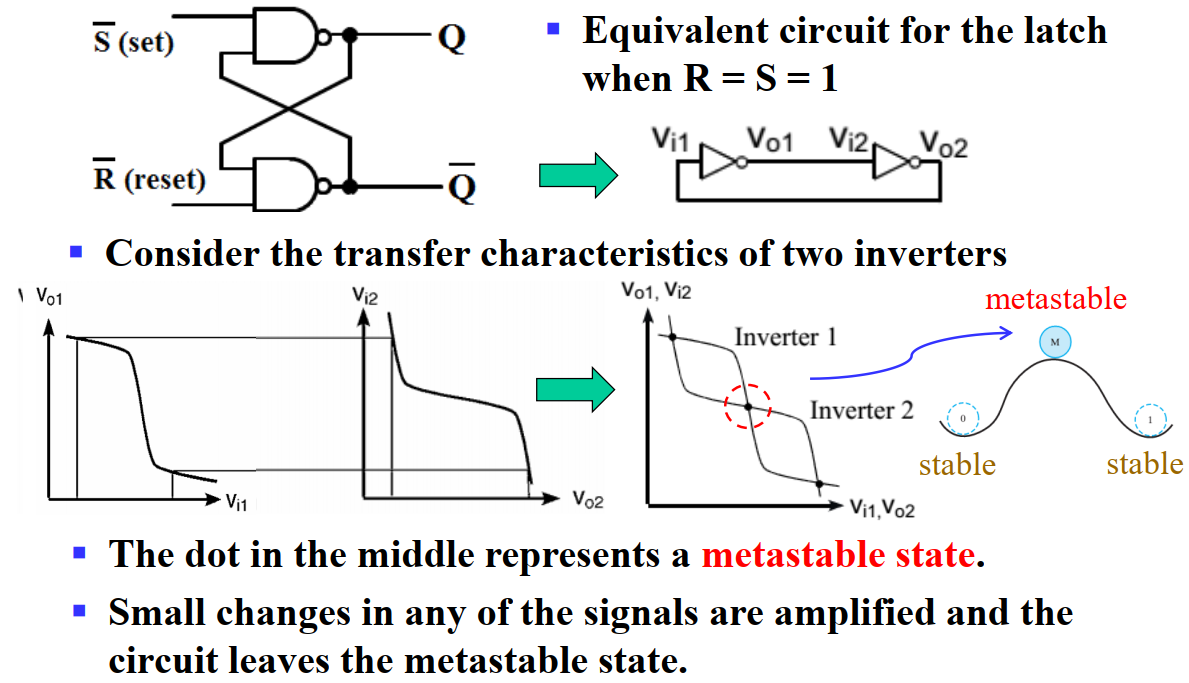
为了让锁存器稳定,我们要避免振荡(oscillation)和亚稳态(metastable)。这要求我们不同时将 S 和 R 置 1,且改变输入时确保结果已经稳定。
SR & S'R' 锁存器 | SR & S'R' Latch¶
SR 锁存器和 S'R' 锁存器的基本原理是一致的,只不过前者用的是或非门,后者用的是与非门。
SR 锁存器和 S'R' 锁存器的输入都是 S(Set) 和 R(Reset) 两个部分,输出都是 Q 和 Q' 两个部分。
名称上 的共同点是,当 S 为
1时,Q 都会是1;对于 R 和 Q' 也是这样,只不过要注意,S'R'锁存器输入的并不是这里所说的 S,而是将 S' 作为输入。


这两个电路都属于异步电路。
一个记忆方法是,SR 的门元件对 1 敏感,所以是 或非门 的实现;而 S'R' 的门元件对 0 敏感,所以是 与非门 的实现。而通过 「当 S 为 1 时,Q 都会是 1」可以得到 S、R 与 Q、Q' 的位置。
但是实际的存储元件并不是单纯的 SR/S'R' Latches,因为后者容易受到毛刺信号干扰。所以我们需要将该电路改进。
我们改进电路并添加使能端,得到带控制输入的 SR 锁存器(SR Latch with Control Input)(S'R'略),这里的控制输入是 C(Control),若为时钟脉冲,则此时电路为同步电路。

注意!
SR 锁存器通过 或非门 实现,但带输入控制的 SR 锁存器则通过 与非门 实现!
D 锁存器 | D Latch¶
D 锁存器实际上是带控制输入的 SR 锁存器的改进。
我们关注到,即使是带控制输入的 SR 锁存器,也存在一个「undefined」状态,而这是我们不希望出现的。为了避免这种情况的发生,我们可以直接强制要求 \(S = \overline R\),于是就避免了 undefined 情况的出现,而电路中 C 的存在保证了原来的0,0 。我们称之为 D 锁存器,电路图如下:

只有当 C 为 1 时,D 锁存器才能写入数据;而当 C 为 0 时,D 锁存器的数据就不会变化。
透明的危害:空翻
当然,D 锁存器也存在问题。如果我门将 \(\overline Q\) 接到 D 上,就会发现 D 锁存器将不停的变化其中的数据,出现 空翻,导致我们无法确定 C 置 0 时 Q 的输出究竟是什么,而这是非常危险的。
这主要是因为 D 锁存器的输入和输出都是直接暴露出来、同时允许变化的(不是同时变化,是指在 Input 可以变的时候 Output 也能变),即 透明(transparent) 的。这就导致了在一个时钟周期里,同时存在 可以互相影响 的两个东西。这也是触发器所解决的问题。
触发器 | Flip-Flop¶
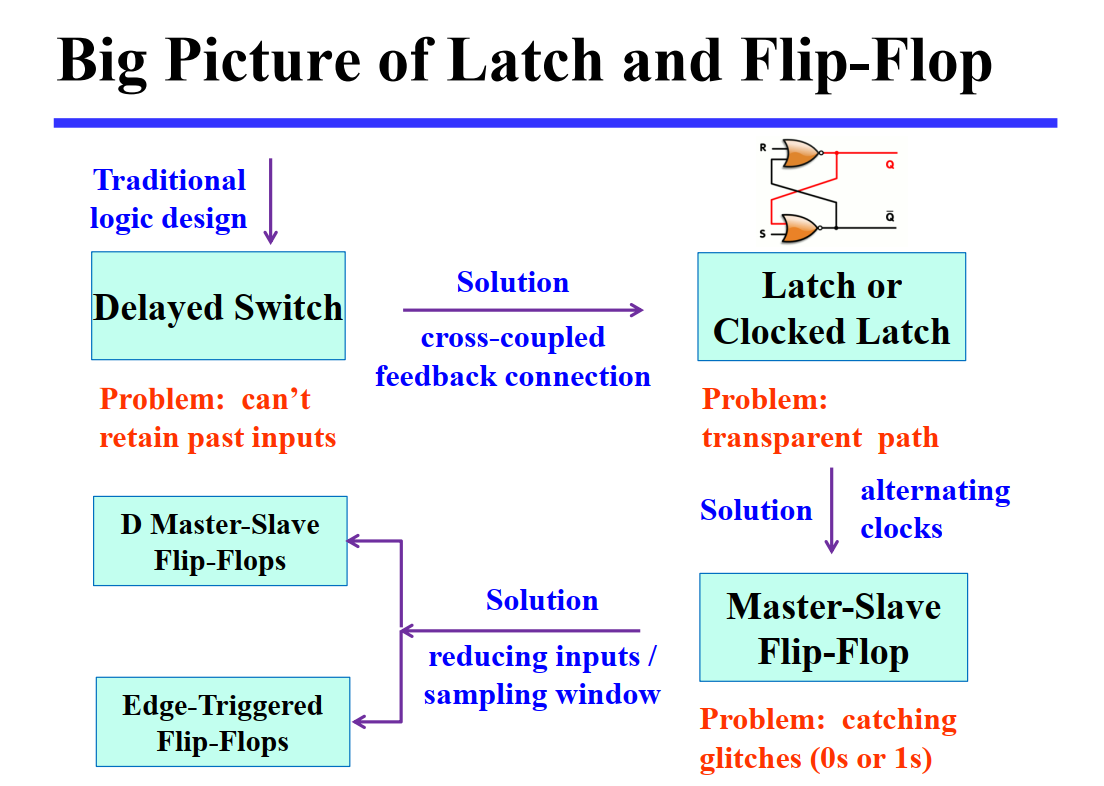
为了解决上面提到的,由「透明」引发的问题,而采用触发器的设计。通过组合两个锁存器,主要有两种实现方法:
- 在有脉冲(高电平)时,修改第一个锁存器的值,保持第二个锁存器的值;在没有脉冲(低电平)时候保持第一个锁存器的值,修改第二个锁存器的值,更新触发器的状态,即 主从式(master-slave)触发器;
- 仅在时钟的边缘触发,即在特定时刻仅接受一个输入,即 边沿触发式(edge-triggered)触发器;
边沿触发式 D 触发器是目前使用最广泛的触发器。
SR 主从触发器 | SR Master-Slave Flip-Flop¶

这个能解决上述问题,是因为二者的时钟脉冲是相反的,所以在一个时钟周期内,只有一个锁存器是可以变化的的,而另一个是保持的。Master触发器采样数据,Slave触发器展示状态。
在上升沿的时候,Master 触发器可能会采样到毛刺(Glitch),导致出现错误的状态。这个行为叫做 (1s 采样)1s catch

边沿触发式触发器 | Edge-Triggered Flip-Flop¶
为了解决上面最后的毛刺问题,我们可以将输入端减半,使用 D master-slave FF,在 Master 触发器的输入端加上一个 同步(synchronizer),即将输入信号通过一个 D 锁存器,这样就能够保证输入信号的稳定性。
但此时还是有一个输入窗口,还是会发生干扰。所以,我们缩小输入窗口,使用 Edge-Triggered FF。边缘触发触发器仅在时钟信号的过渡期间触发——当脉冲处于恒定电平时,边缘触发触发器忽略脉冲。
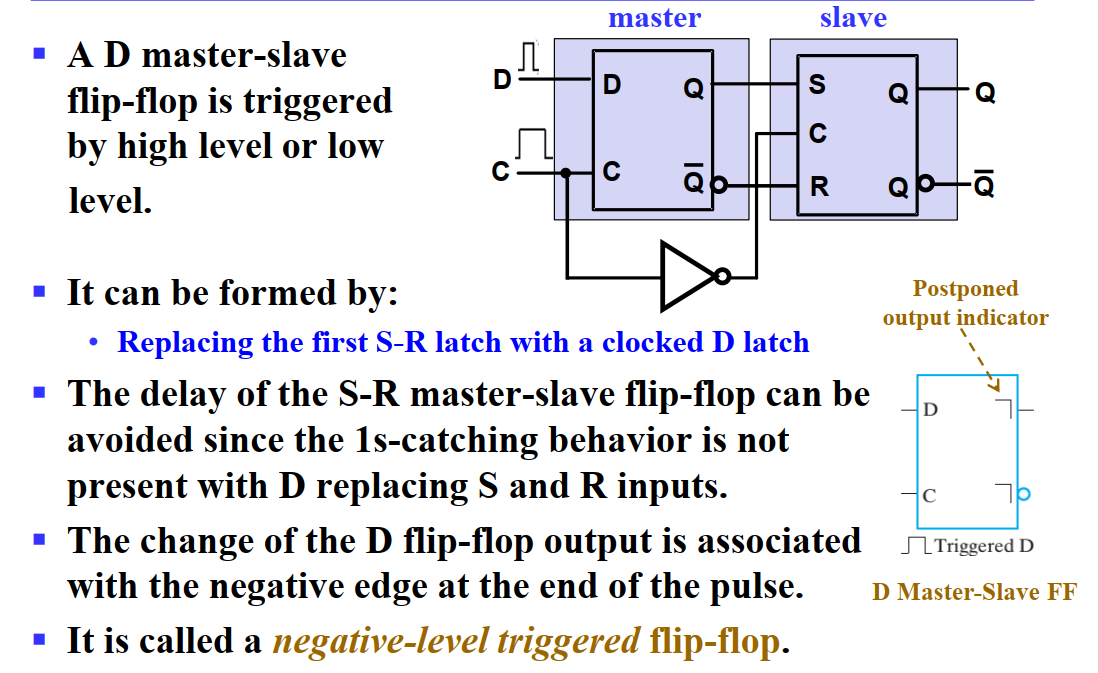
上图右下角的图示中,下方的凸起表示高电平采样;“┐”表示输出信号的延迟,即输出信号在采样结束后才会发生变化。这里也就是说,输出信号在时钟下降沿后才会发生变化。所以称其为 negative-edge-triggered FF(负边沿触发式触发器)。
与之相对应的,我们还有正边沿触发 D 触发器。
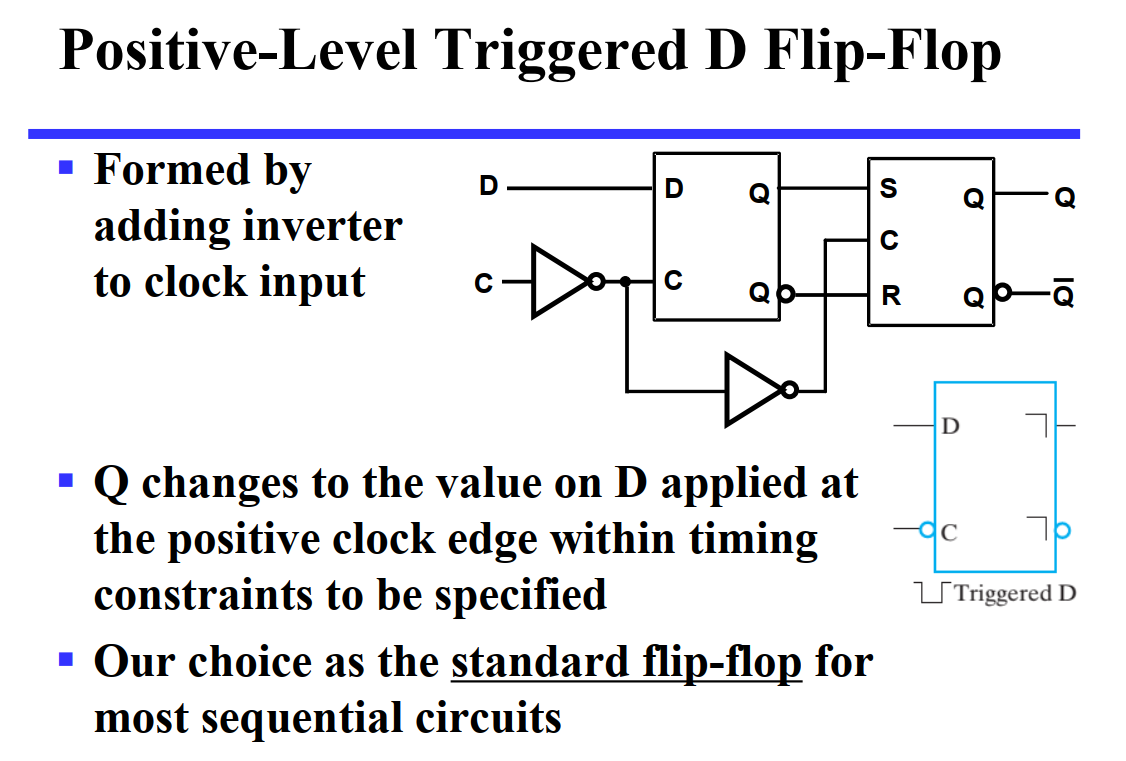
关注上升沿前后,上升沿前一刻,主锁存器可写,从锁存器只读;上升沿后一刻,主锁存器只读,从锁存器只写,且写入的是主锁存器存储的值——换句话来说,存的是上升沿前一刻写入主锁存器的内容。
而它为什么能做到边缘采样?因为它的内部结构为:
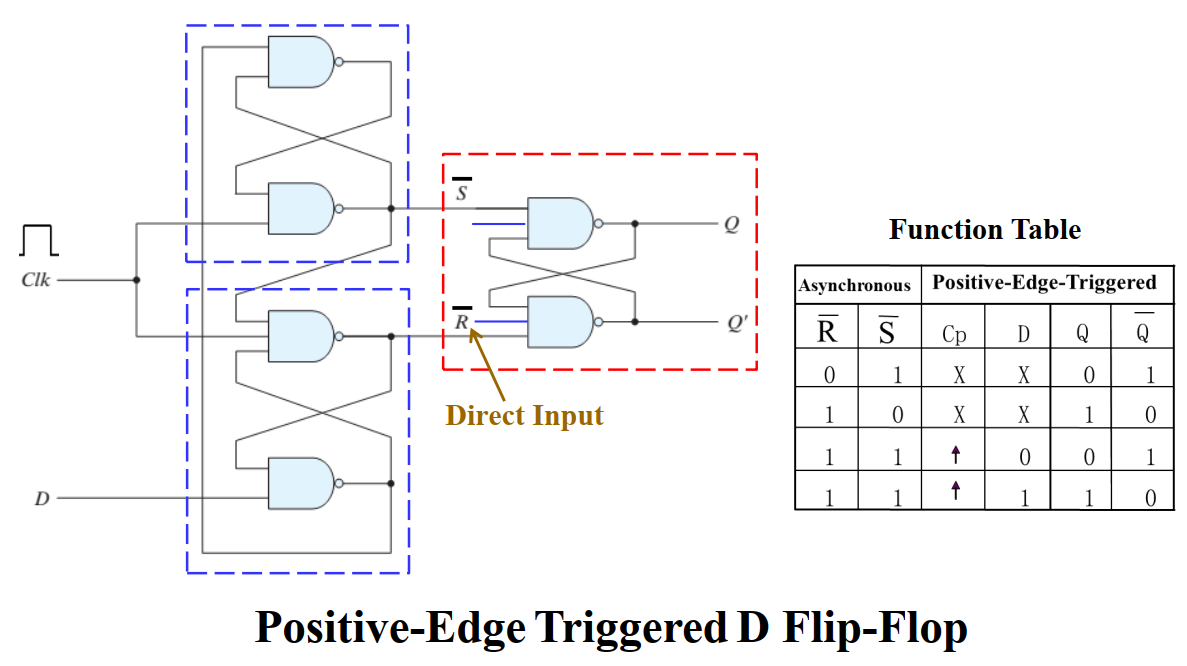
需要注意的一点是,D 触发器没有「保持」态。如果要使 D 触发器保持,可以使时钟脉冲失效或通过 MUX 将输出接到输入实现。其中前者不太常用,因为受门控的时钟脉冲进入触发器时有延迟,即 时钟偏移(clock skew)
标准图形符号¶

带尖尖的三角形的表示边沿采样
直接输入 | Direct Inputs¶
这些直接输入往往是异步的,一般用来异步置位(直接置位或预置)或异步复位(直接复位或清零)。
对于时序电路来说,「复位」或「置位」这种输入常常作为初始化,即确定各个触发器的「初始状态」。
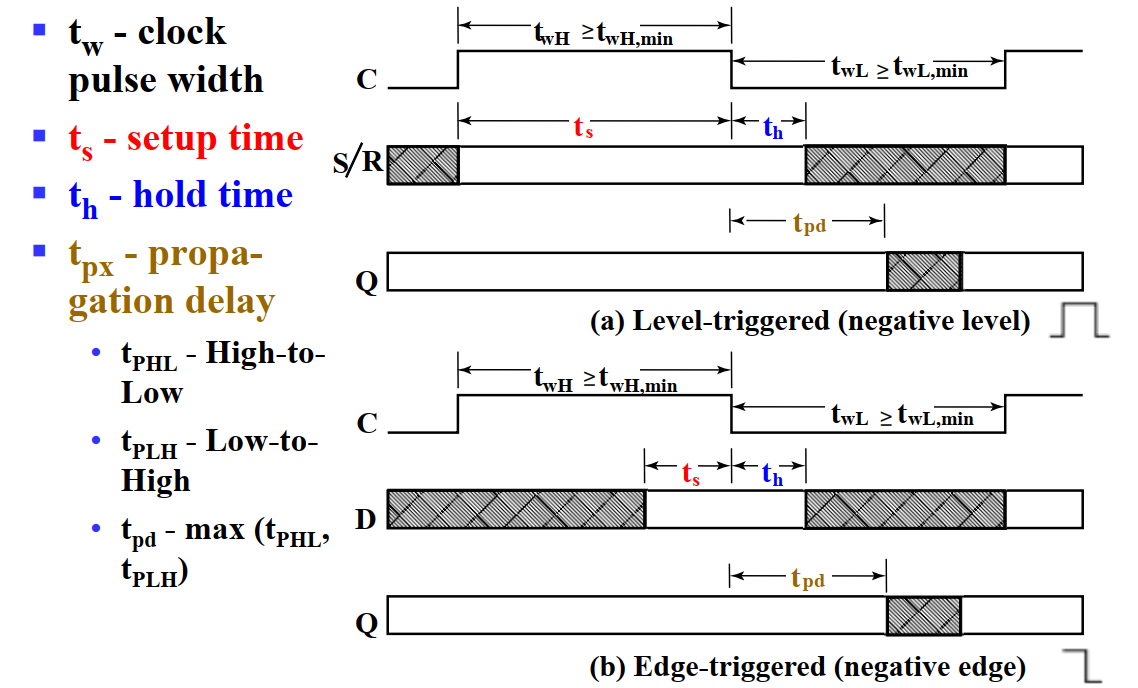
触发器的时序参数 | Flip-Flop Timing Parameters¶
Setup Time:在时钟信号的上升沿之前,输入信号必须保持稳定的时间。
Hold Time:在时钟信号的上升沿之后,输入信号必须保持稳定的时间。
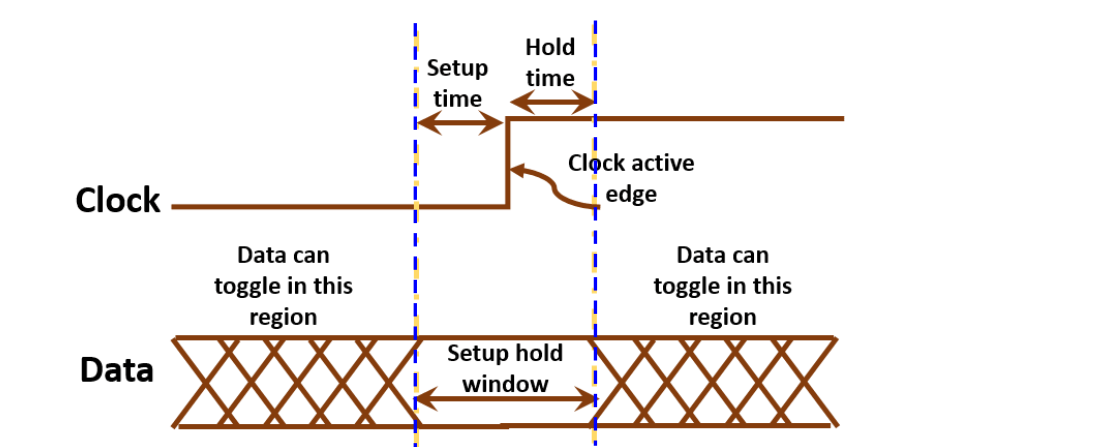
如果数据在 "setup-hold-window" 内发生变化,则输出是不可预测的或亚稳态的。
时序电路分析 | Sequential Circuit Analysis¶
时序电路的分析包括:
- 用状态表、状态图和输入/输出布尔方程生成时序电路的功能
- 确定时序电路必须满足的时序约束,以防止亚稳态,从而使电路可以无误地使用
时序电路的分析过程主要包括:
- 推导输入方程、下一状态方程和输出方程
- 推导状态表(带状态的真值表):
- 输入:电路的输入、电路的当前状态
- 输出:电路的输出、所有触发器的下一状态
- 列出时序电路的下一状态
- 得到状态图
- 分析电路的性能
- 验证电路的正确性,检查自恢复能力并绘制时序参数
为了分析时序电路,我们需要一些工具来表示时序电路的一些特征与逻辑。观察时序电路和组合电路的区别,发现最核心的就是逻辑运算过程中出现了「状态」参与运算。因此,我们需要在各个组合电路分析中采用的表示方法中,添加表示「状态」的信息。
除此之外,如果只是单纯的将「状态」作为一个新的输入,作为增量添加到表达方式中,会发现这些表述会显得很重。所以我们也需要寻找一种更好的办法来表达时序电路中的逻辑,这就是「状态图」。
触发器的输入方程 | Flip-Flop Input Equation¶
触发器的输入方程(flip-flop input equation) 主要是为其提供一个代数表达方式。它的主要想法是:
- 表达每一个触发器的输入与输出之间的关系;
- 表达每一个直接输出的逻辑表达式。其中,触发器的输出符号表示了其类型(即符号)与输出(即下标)。
具体来说,例如下面这个电路:

可以发现,其中包含两个触发器 \(D_A\) 和 \(D_B\),以及一个组合逻辑输出 \(Y\),因而可以根据电路的特征,得到下面这几个式子:
状态表 | State Table¶
当然,时序电路的逻辑有时候也可以通过状态表来描述,只不过与组合电路的 真值表 不同,状态表(state table) 有四栏:当前状态(present state)、输入(input)、下一状态(next state)、输出(output)。其含义是比较显然的,只不过需要通过电路图得到状态表,需要首先得到「当前状态」向「下一状态」转移的方程,即对于某个时刻 \(t\) 的触发器 \(A\) 的输出 \(A(t)\),需要得到它下一刻的状态 \(A(t+1) = f(A(t), ...)\)。
同样以这个电路为 🌰:

首先我们对 \(D_A\) 得到转移方程:\(A(t+1) = D_A(t) = A(t)X(t) + B(t)X(t)\)。类似地也能得到 \(B\) 的转移方程。
于是,根据这些信息,我们可以写出它的状态表:
Present StateA(t) B(t) |
InputX(t) |
Next StateA(t+1) B(t+1) |
OutputY(t) |
|---|---|---|---|
0 0 |
0 |
0 0 |
0 |
0 0 |
1 |
0 1 |
0 |
0 1 |
0 |
0 0 |
1 |
0 1 |
1 |
1 1 |
0 |
1 0 |
0 |
0 0 |
1 |
1 0 |
1 |
1 0 |
0 |
1 1 |
0 |
0 0 |
1 |
1 1 |
1 |
1 0 |
0 |
Mealy model circuit & Moore model circuit
如果输出既依赖于当前状态,也依赖于输入的时序电路,则称为 米勒型电路(Mealy model circuit);而如果输出只依赖于当前状态,则称为 摩尔型电路(Moore model circuit)。
在 状态图 中,我们还将再一次遇到这两个人名。
状态图 | State Diagram¶
可以发现,状态表比较清晰的表达了不同的状态和输入得到的结果,但是对于「不同状态之间是如何转换的」这件事的描述并不清晰。而对于「联系」这件事,有向图是一个非常好的形式,所以我们将介绍 状态图(state diagram)。
状态图承载的信息量和状态表是一样的,所以也是需要表达 当前状态(present state)、输入(input)、下一状态(next state)、输出(output) 这四个东西。只不过「下一状态」是通过有向边来表示的。当前状态作为一个 node 的属性;而输入作为 edge 的一个属性;至于输出,根据它是放在 edge 上还是 node 上,分为 米勒型(Mealy) 和 摩尔型(Moore) 两种。
Mealy
例如,这是一个 米勒型 的状态图,以及对应的状态表。

因为米勒型电路的 输出与当前状态和输入都有关,所以输出会和输入一起放在 edge 里。
对于米勒型,node 内的二进制为 present state 中的 AB;edge 上分别为 input / output:X/Y;有向边表达了每个状态在特定输入下的下一个状态。
例如,关注 node 00,它有一条自环 0/0,对应 状态表 的第一行;它有一条 edge 1/0 指向 node 01,对应 状态表的第二行。

当然,米勒型是有 缺陷 的,在时序电路设计之后的步骤中,我们需要根据它来对每一个状态设计输出方程。此时由于两个输出共享同一个目标状态,所以我们需要将两个输出结合到同一个式子中,这将提高设计难度和组合电路成本。
Moore
而下面是一个 摩尔型 的状态图,以及对应的状态表。

因为摩尔型电路的 输出只与当前状态有关,所以输出会和当前状态放在一起,即放在 node 里。
对于摩尔型,node 内的二进制表示 present state / output:A/Z;edge 上列举了这种转移可能的 inputs:XY。
例如,关注 node 0/0,它有两条自环 00 和 11,分别对应 状态表 的第一行和第四行;它有两条 edge 01 和 10 指向 node 1/1,对应 状态表 的第二行和第三行。

摩尔型也存在 缺陷 的,非常显然,相比于米勒型,摩尔型需要更多的状态。
换句话来说,米勒型倾向于表达「在特定状态下,特定输入将导致某种结果,以及状态转移」;而摩尔型倾向于表达「特定输入将导致某个状态向另外一个状态转移,而输出更像是一种状态的结果」。
状态图还有进阶形态,之后会提及,就是 状态机。
等价状态¶
同一输入序列下,输出序列相同的两个状态是等价的,换句话来说,如果两个状态的输出序列相同,且在每一个输入下,它们的下一状态也相同或等价,则这两个状态是等价的。
例如下图中的 S2 和 S3 就是等价的。
我们可以消去等价状态,从而简化状态图。