跳转至

时间复杂度

约 2709 个字 291 行代码 预计阅读时间 17 分钟

运行时间可以直观且准确地反映算法的效率。如果我们想要准确预估一段代码的运行时间，应该如何操作呢？

  1. 确定运行平台，包括硬件配置、编程语言、系统环境等，这些因素都会影响代码的运行效率。
  2. 评估各种计算操作所需的运行时间，例如加法操作 + 需要 1 ns ，乘法操作 * 需要 10 ns ，打印操作 print() 需要 5 ns 等。
  3. 统计代码中所有的计算操作，并将所有操作的执行时间求和，从而得到运行时间。

例如在以下代码中，输入数据大小为 \(n\) ：

// 在某运行平台下
void algorithm(int n) {
    int a = 2;  // 1 ns
    a = a + 1;  // 1 ns
    a = a * 2;  // 10 ns
    // 循环 n 次
    for (int i = 0; i < n; i++) {   // 1 ns ，每轮都要执行 i++
        printf("%d", 0);            // 5 ns
    }
}

根据以上方法，可以得到算法运行时间为 \(6n + 12\) ns ：

\[ 1 + 1 + 10 + (1 + 5) \times n = 6n + 12 \]

但实际上，统计算法的运行时间既不合理也不现实。首先，我们不希望将预估时间和运行平台绑定，因为算法需要在各种不同的平台上运行。其次，我们很难获知每种操作的运行时间，这给预估过程带来了极大的难度。

统计时间增长趋势

时间复杂度分析统计的不是算法运行时间，而是算法运行时间随着数据量变大时的增长趋势。

“时间增长趋势”这个概念比较抽象，我们通过一个例子来加以理解。假设输入数据大小为 \(n\) ，给定三个算法函数 A、B 和 C ：

// 算法 A 的时间复杂度：常数阶
void algorithm_A(int n) {
    printf("%d", 0);
}
// 算法 B 的时间复杂度：线性阶
void algorithm_B(int n) {
    for (int i = 0; i < n; i++) {
        printf("%d", 0);
    }
}
// 算法 C 的时间复杂度：常数阶
void algorithm_C(int n) {
    for (int i = 0; i < 1000000; i++) {
        printf("%d", 0);
    }
}

下图展示了以上三个算法函数的时间复杂度。

  • 算法 A 只有 \(1\) 个打印操作，算法运行时间不随着 \(n\) 增大而增长。我们称此算法的时间复杂度为“常数阶”。
  • 算法 B 中的打印操作需要循环 \(n\) 次，算法运行时间随着 \(n\) 增大呈线性增长。此算法的时间复杂度被称为“线性阶”。
  • 算法 C 中的打印操作需要循环 \(1000000\) 次，虽然运行时间很长，但它与输入数据大小 \(n\) 无关。因此 C 的时间复杂度和 A 相同，仍为“常数阶”。

算法 A、B 和 C 的时间增长趋势

相较于直接统计算法运行时间，时间复杂度分析有哪些特点呢？

  • 时间复杂度能够有效评估算法效率。例如，算法 B 的运行时间呈线性增长，在 \(n > 1\) 时比算法 A 更慢，在 \(n > 1000000\) 时比算法 C 更慢。事实上，只要输入数据大小 \(n\) 足够大，复杂度为“常数阶”的算法一定优于“线性阶”的算法，这正是时间增长趋势所表达的含义。
  • 时间复杂度的推算方法更简便。显然，运行平台和计算操作类型都与算法运行时间的增长趋势无关。因此在时间复杂度分析中，我们可以简单地将所有计算操作的执行时间视为相同的“单位时间”，从而将“计算操作的运行时间的统计”简化为“计算操作的数量的统计”，这样一来估算难度就大大降低了。
  • 时间复杂度也存在一定的局限性。例如，尽管算法 A 和 C 的时间复杂度相同，但实际运行时间差别很大。同样，尽管算法 B 的时间复杂度比 C 高，但在输入数据大小 \(n\) 较小时，算法 B 明显优于算法 C 。在这些情况下，我们很难仅凭时间复杂度判断算法效率的高低。当然，尽管存在上述问题，复杂度分析仍然是评判算法效率最有效且常用的方法。

函数渐近上界

给定一个输入大小为 \(n\) 的函数：

void algorithm(int n) {
    int a = 1;  // +1
    a = a + 1;  // +1
    a = a * 2;  // +1
    // 循环 n 次
    for (int i = 0; i < n; i++) {   // +1（每轮都执行 i ++）
        printf("%d", 0);            // +1
    }
}

设算法的操作数量是一个关于输入数据大小 \(n\) 的函数，记为 \(T(n)\) ，则以上函数的的操作数量为：

\[ T(n) = 3 + 2n \]

\(T(n)\) 是一次函数，说明其运行时间的增长趋势是线性的，因此它的时间复杂度是线性阶。

我们将线性阶的时间复杂度记为 \(O(n)\) ，这个数学符号称为「大 \(O\) 记号 big-\(O\) notation」，表示函数 \(T(n)\) 的「渐近上界 asymptotic upper bound」。

时间复杂度分析本质上是计算“操作数量函数 \(T(n)\)”的渐近上界，其具有明确的数学定义。

函数渐近上界

若存在正实数 \(c\) 和实数 \(n_0\) ，使得对于所有的 \(n > n_0\) ，均有 \(T(n) \leq c \cdot f(n)\) ，则可认为 \(f(n)\) 给出了 \(T(n)\) 的一个渐近上界，记为 \(T(n) = O(f(n))\) 。

如下图所示，计算渐近上界就是寻找一个函数 \(f(n)\) ，使得当 \(n\) 趋向于无穷大时，\(T(n)\) 和 \(f(n)\) 处于相同的增长级别，仅相差一个常数项 \(c\) 的倍数。

函数的渐近上界

最差、最佳、平均时间复杂度

算法的时间效率往往不是固定的，而是与输入数据的分布有关。假设输入一个长度为 \(n\) 的数组 nums ，其中 nums 由从 \(1\) 至 \(n\) 的数字组成，每个数字只出现一次；但元素顺序是随机打乱的，任务目标是返回元素 \(1\) 的索引。我们可以得出以下结论。

  • 当 nums = [?, ?, ..., 1] ，即当末尾元素是 \(1\) 时，需要完整遍历数组，达到最差时间复杂度 \(O(n)\) 。
  • 当 nums = [1, ?, ?, ...] ，即当首个元素为 \(1\) 时，无论数组多长都不需要继续遍历，达到最佳时间复杂度 \(\Omega(1)\) 。

“最差时间复杂度”对应函数渐近上界，使用大 \(O\) 记号表示。相应地，“最佳时间复杂度”对应函数渐近下界，用 \(\Omega\) 记号表示：

/* 生成一个数组，元素为 { 1, 2, ..., n }，顺序被打乱 */
int *randomNumbers(int n) {
    // 分配堆区内存（创建一维可变长数组：数组中元素数量为 n ，元素类型为 int ）
    int *nums = (int *)malloc(n * sizeof(int));
    // 生成数组 nums = { 1, 2, 3, ..., n }
    for (int i = 0; i < n; i++) {
        nums[i] = i + 1;
    }
    // 随机打乱数组元素
    for (int i = n - 1; i > 0; i--) {
        int j = rand() % (i + 1);
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    return nums;
}

/* 查找数组 nums 中数字 1 所在索引 */
int findOne(int *nums, int n) {
    for (int i = 0; i < n; i++) {
        // 当元素 1 在数组头部时，达到最佳时间复杂度 O(1)
        // 当元素 1 在数组尾部时，达到最差时间复杂度 O(n)
        if (nums[i] == 1)
            return i;
    }
    return -1;
}

值得说明的是，我们在实际中很少使用最佳时间复杂度，因为通常只有在很小概率下才能达到，可能会带来一定的误导性。而最差时间复杂度更为实用，因为它给出了一个效率安全值，让我们可以放心地使用算法。

从上述示例可以看出，最差或最佳时间复杂度只出现于“特殊的数据分布”，这些情况的出现概率可能很小，并不能真实地反映算法运行效率。相比之下，平均时间复杂度可以体现算法在随机输入数据下的运行效率，用 \(\Theta\) 记号来表示。

对于部分算法，我们可以简单地推算出随机数据分布下的平均情况。比如上述示例，由于输入数组是被打乱的，因此元素 \(1\) 出现在任意索引的概率都是相等的，那么算法的平均循环次数就是数组长度的一半 \(n / 2\) ，平均时间复杂度为 \(\Theta(n / 2) = \Theta(n)\) 。

但对于较为复杂的算法，计算平均时间复杂度往往是比较困难的，因为很难分析出在数据分布下的整体数学期望。在这种情况下，我们通常使用最差时间复杂度作为算法效率的评判标准。

为什么很少看到 \(\Theta\) 符号？

可能由于 \(O\) 符号过于朗朗上口，我们常常使用它来表示平均时间复杂度。但从严格意义上看，这种做法并不规范。在本笔记和其他资料中，若遇到类似“平均时间复杂度 \(O(n)\)”的表述，请将其直接理解为 \(\Theta(n)\) 。

推算方法

渐近上界的数学味儿有点重，如果你感觉没有完全理解，也无须担心。因为在实际使用中，我们只需要掌握推算方法，数学意义就可以逐渐领悟。

根据定义，确定 \(f(n)\) 之后，我们便可得到时间复杂度 \(O(f(n))\) 。那么如何确定渐近上界 \(f(n)\) 呢？总体分为两步：首先统计操作数量，然后判断渐近上界。

非递归程序

第一步：统计操作数量

针对代码，逐行从上到下计算即可。然而，由于上述 \(c \cdot f(n)\) 中的常数项 \(c\) 可以取任意大小，因此操作数量 \(T(n)\) 中的各种系数、常数项都可以被忽略。根据此原则，可以总结出以下计数简化技巧。

  1. 忽略 \(T(n)\) 中的常数项。因为它们都与 \(n\) 无关，所以对时间复杂度不产生影响。
  2. 省略所有系数。例如，循环 \(2n\) 次、\(5n + 1\) 次等，都可以简化记为 \(n\) 次，因为 \(n\) 前面的系数对时间复杂度没有影响。
  3. 循环嵌套时使用乘法。总操作数量等于外层循环和内层循环操作数量之积，每一层循环依然可以分别套用第 1 点和第 2 点的技巧。

给定一个函数，我们可以用上述技巧来统计操作数量。

void algorithm(int n) {
    int a = 1;  // +0（技巧 1）
    a = a + n;  // +0（技巧 1）
    // +n（技巧 2）
    for (int i = 0; i < 5 * n + 1; i++) {
        printf("%d", 0);
    }
    // +n*n（技巧 3）
    for (int i = 0; i < 2 * n; i++) {
        for (int j = 0; j < n + 1; j++) {
            printf("%d", 0);
        }
    }
}

以下公式展示了使用上述技巧前后的统计结果，两者推出的时间复杂度都为 \(O(n^2)\) 。

\[ \begin{aligned} T(n) & = 2n(n + 1) + (5n + 1) + 2 & \text{完整统计 (-.-|||)} \newline & = 2n^2 + 7n + 3 \newline T(n) & = n^2 + n & \text{偷懒统计 (o.O)} \end{aligned} \]

第二步：判断渐近上界

时间复杂度由多项式 \(T(n)\) 中最高阶的项来决定。这是因为在 \(n\) 趋于无穷大时，最高阶的项将发挥主导作用，其他项的影响都可以被忽略。

下表展示了一些例子，其中一些夸张的值是为了强调“系数无法撼动阶数”这一结论。当 \(n\) 趋于无穷大时，这些常数变得无足轻重。

操作数量 \(T(n)\) 时间复杂度 \(O(f(n))\)
\(100000\) \(O(1)\)
\(3n + 2\) \(O(n)\)
\(2n^2 + 3n + 2\) \(O(n^2)\)
\(n^3 + 10000n^2\) \(O(n^3)\)
\(2^n + 10000n^{10000}\) \(O(2^n)\)

递归：主定理 | Master Theorem

前文中都是针对迭代算法进行讨论的，通过代码能容易得出操作数量 \(T(n)\) ，从而推算出时间复杂度 \(O(f(n))\) 。但对于递归算法，我们该如何分析时间复杂度呢？

主定理: 若\(a\),\(b\) 是常数,\(f(n)\) 为额外附加值函数,\(T(n)\) 为递归式\(T(n) = aT(\frac{n}{b}) + f(n)\) \((a>0, b>1)\),则有:

  1. 当 \(f(n) = O(n^{\log_b a -\epsilon})\) 其中 \(\epsilon > 0\) 是一个常数(相当于 \(\log_b a > f(n)\)),则有 \(T(n) = \Theta(n^{\log_b a})\)

  2. 当 \(f(n) = \Theta(n^{\log_b a})\),则有 \(T(n) = \Theta(n^{\log_b a}\log n)\)

  3. 当 \(f(n) = \Omega(n^{\log_b a} + \epsilon)\) 其中 \(\epsilon > 0\) 是常数(相当于 \(\log_b a < f(n)\)),且对于一个常数 \(c < 1\) 和所有足够大的 \(n\) 有 \(af(\frac{n}{b}) \leq cf(n)\)(这一条件在这里可以暂时略过,但在证明时起到至关重要的作用),则有 \(T(n) = \Theta(f(n))\)

  4. 当 \(f(n) = \Theta(n^{\log_b a}\log^k n)\) 其中 \(k \geq 1\) 是常数,则有 \(T(n) = \Theta(n^{\log_b a}\log^{k+1} n)\)

我们一般只会碰到前三种情况，进行总结，有： Alt text

\(T ( N ) = 2 T( N/2 ) + c N ,T(1) = O(1)\)

此时\(a=2,b=2,d=1\)，有\(d = \log_b a\)，所以是图中第二种情况，即\(T(n) = \Theta(n\log n)\)

例子 | MaxSubsequenceSum

虽然给的例子是Subsequence，实际上更好的说法应该是Substring。因为前者不要求连续，后者要求连续。我们接下来处理的都是连续形式的。

Given (possibly negative) integers \(A_1\), \(A_2\), …, \(A_N\), find the maximum value of \(\sum\limits_{k=i}\limits^jA_k\)

算法一

int MaxSubsequenceSum(const int A[], int N)
{
    int ThisSum, MaxSum, i, j, k;
    MaxSum = 0;                 /* initialize the maximum sum */
    for (i = 0; i < N; i++)     /* start from A[i] */
        for (j = i; j < N; j++) /* end at A[j] */
        {
            ThisSum = 0;
            for (k = i; k <= j; k++)
                ThisSum += A[k]; /* sum from A[i] to A[j] */
            if (ThisSum > MaxSum)
                MaxSum = ThisSum; /* update max sum */
        }                         /* end for-j and for-i */
    return MaxSum;
}

易知合理。计算得到这个算法的复杂度为\(O(N^3)\)

算法二

int MaxSubsequenceSum(const int A[], int N)
{
    int ThisSum, MaxSum, i, j;
    MaxSum = 0;             /* initialize the maximum sum */
    for (i = 0; i < N; i++) /* start from A[i] */
    {
        ThisSum = 0;
        for (j = i; j < N; j++)
        {                    /* end at A[j] */
            ThisSum += A[j]; /* sum from A[i] to A[j] */
            if (ThisSum > MaxSum)
                MaxSum = ThisSum; /* update max sum */
        }                         /* end for-j */
    }                             /* end for-i */
    return MaxSum;
}
易知合理。计算得到这个算法的复杂度为\(O(N^2)\)

算法三

Divide and Conquer
int Max3(int a, int b, int c)
{
    int max;
    if (a > b)
        max = a;
    else
        max = b;
    if (c > max)
        max = c;
    return max;
}

static int MaxSubSum(const int A[], int Left, int Right)
{
    int MaxLeftSum, MaxRightSum;
    int MaxLeftBorderSum, MaxRightBorderSum;
    int LeftBorderSum, RightBorderSum;
    int Center, i;
    if (Left == Right) /* Base Case */
        if (A[Left] > 0)
            return A[Left];
        else
            return 0;

    Center = (Left + Right) / 2;
    MaxLeftSum = MaxSubSum(A, Left, Center);       // 递归求左边最大子序列和
    MaxRightSum = MaxSubSum(A, Center + 1, Right); // 递归求右边最大子序列和

    // 求跨越中点的最大子序列和
    MaxLeftBorderSum = 0;
    LeftBorderSum = 0;
    for (i = Center; i >= Left; i--)
    {
        LeftBorderSum += A[i];
        if (LeftBorderSum > MaxLeftBorderSum)
            MaxLeftBorderSum = LeftBorderSum;
    }

    MaxRightBorderSum = 0;
    RightBorderSum = 0;
    for (i = Center + 1; i <= Right; i++)
    {
        RightBorderSum += A[i];
        if (RightBorderSum > MaxRightBorderSum)
            MaxRightBorderSum = RightBorderSum;
    }

    return Max3(MaxLeftSum, MaxRightSum,
                MaxLeftBorderSum + MaxRightBorderSum);
}

我们来分析一下这个问题， 我们先把数组平均分成左右两部分。

此时有三种情况：

  1. 最大子序列全部在数组左部分
  2. 最大子序列全部在数组右部分
  3. 最大子序列横跨左右数组

对于前两种情况，我们相当于将原问题转化为了规模更小的同样问题。

对于第三种情况，由于已知循环的起点（即中点），我们只需要进行一次循环，分别找出左边和右边的最大子序列即可。

所以一个思路就是我们每次都对数组分成左右两部分，然后分别计算上面三种情况的最大子序列和，取出最大的即可。

举例说明，如下图： Alt text

所以\(T ( N ) = 2 T( N/2 ) + c N ,T(1) = O(1)\)，在之前的主定理部分，我们已经知道这个算法的复杂度为\(O(N\log N)\)

算法四

On-line Algorithm
int MaxSubsequenceSum(const int A[], int N)
{
    int ThisSum, MaxSum, j;
    ThisSum = MaxSum = 0;
    for (j = 0; j < N; j++)
    {
        ThisSum += A[j];
        if (ThisSum > MaxSum)
            MaxSum = ThisSum;
        else if (ThisSum < 0)
            ThisSum = 0;
    }
    return MaxSum;
}
因为该问题不需要最大序列和的坐标输出，所以我们不需要记忆序列位置，仅仅记忆当前最大序列和的值即可。该算法只对数据进行一次扫描，一旦A[i]被读入并被处理，不再需要被记忆。

容易分析得到，这个算法的复杂度为\(O(N)\)

常见类型

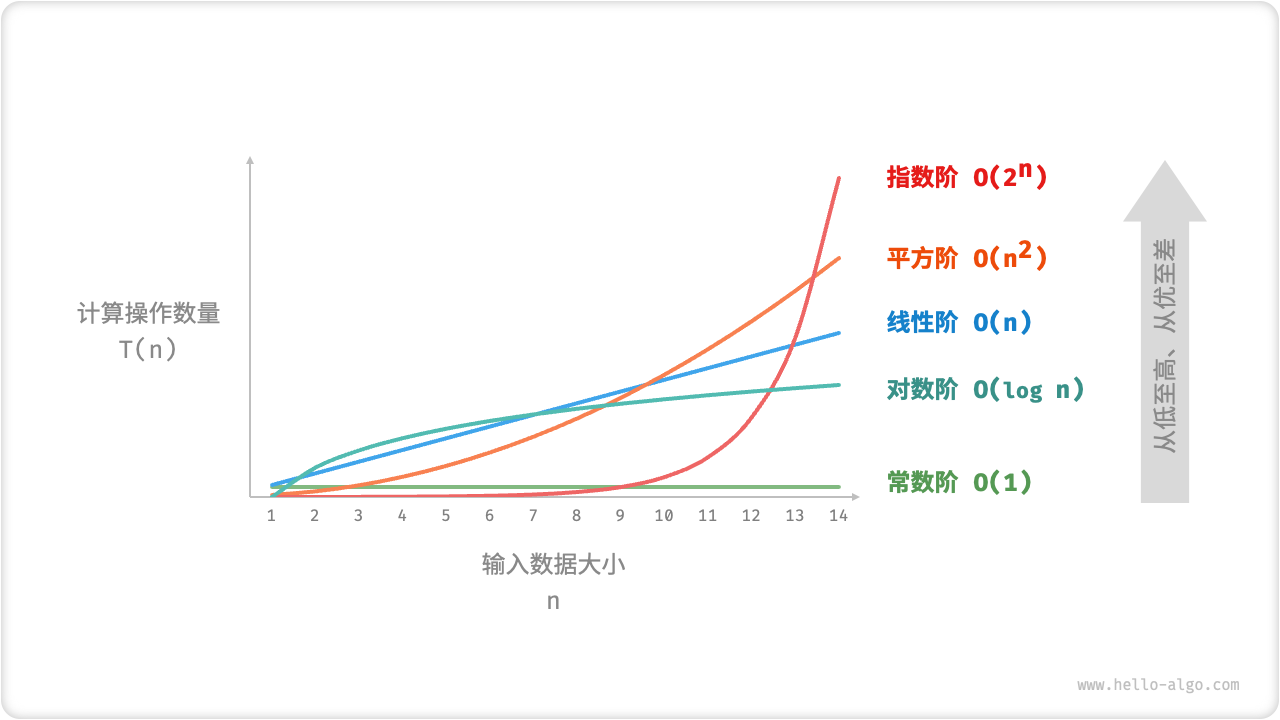
设输入数据大小为 \(n\) ，常见的时间复杂度类型如下图所示（按照从低到高的顺序排列）。

\[ \begin{aligned} O(1) < O(\log n) < O(n) < O(n \log n) < O(n^2) < O(2^n) < O(n!) \newline \text{常数阶} < \text{对数阶} < \text{线性阶} < \text{线性对数阶} < \text{平方阶} < \text{指数阶} < \text{阶乘阶} \end{aligned} \]

常见的时间复杂度类型

常数阶 \(O(1)\)

常数阶的操作数量与输入数据大小 \(n\) 无关，即不随着 \(n\) 的变化而变化。

在以下函数中，尽管操作数量 size 可能很大，但由于其与输入数据大小 \(n\) 无关，因此时间复杂度仍为 \(O(1)\) ：

/* 常数阶 */
int constant(int n) {
    int count = 0;
    int size = 100000;
    int i = 0;
    for (int i = 0; i < size; i++) {
        count++;
    }
    return count;
}

线性阶 \(O(n)\)

线性阶的操作数量相对于输入数据大小 \(n\) 以线性级别增长。线性阶通常出现在单层循环中：

time_complexity.c
/* 线性阶 */
int linear(int n) {
    int count = 0;
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

遍历数组和遍历链表等操作的时间复杂度均为 \(O(n)\) ，其中 \(n\) 为数组或链表的长度：

time_complexity.c
/* 线性阶（遍历数组） */
int arrayTraversal(int *nums, int n) {
    int count = 0;
    // 循环次数与数组长度成正比
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

值得注意的是，输入数据大小 \(n\) 需根据输入数据的类型来具体确定。比如在第一个示例中，变量 \(n\) 为输入数据大小；在第二个示例中，数组长度 \(n\) 为数据大小。

平方阶 \(O(n^2)\)

平方阶的操作数量相对于输入数据大小 \(n\) 以平方级别增长。平方阶通常出现在嵌套循环中，外层循环和内层循环都为 \(O(n)\) ，因此总体为 \(O(n^2)\) ：

    /* 平方阶 */
int quadratic(int n) {
    int count = 0;
    // 循环次数与数组长度成平方关系
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            count++;
        }
    }
    return count;
}

下图对比了常数阶、线性阶和平方阶三种时间复杂度。

常数阶、线性阶和平方阶的时间复杂度

以冒泡排序为例，外层循环执行 \(n - 1\) 次，内层循环执行 \(n-1\)、\(n-2\)、\(\dots\)、\(2\)、\(1\) 次，平均为 \(n / 2\) 次，因此时间复杂度为 \(O((n - 1) n / 2) = O(n^2)\) 。

/* 平方阶（冒泡排序） */
int bubbleSort(int *nums, int n) {
    int count = 0; // 计数器
    // 外循环：未排序区间为 [0, i]
    for (int i = n - 1; i > 0; i--) {
        // 内循环：将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
        for (int j = 0; j < i; j++) {
            if (nums[j] > nums[j + 1]) {
                // 交换 nums[j] 与 nums[j + 1]
                int tmp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = tmp;
                count += 3; // 元素交换包含 3 个单元操作
            }
        }
    }
    return count;
}

指数阶 \(O(2^n)\)

生物学的“细胞分裂”是指数阶增长的典型例子：初始状态为 \(1\) 个细胞，分裂一轮后变为 \(2\) 个，分裂两轮后变为 \(4\) 个，以此类推，分裂 \(n\) 轮后有 \(2^n\) 个细胞。

下图和以下代码模拟了细胞分裂的过程，时间复杂度为 \(O(2^n)\) 。

/* 指数阶（循环实现） */
int exponential(int n) {
    int count = 0;
    int bas = 1;
    // 细胞每轮一分为二，形成数列 1, 2, 4, 8, ..., 2^(n-1)
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < bas; j++) {
            count++;
        }
        bas *= 2;
    }
    // count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
    return count;
}

指数阶的时间复杂度

在实际算法中，指数阶常出现于递归函数中。例如在以下代码中，其递归地一分为二，经过 \(n\) 次分裂后停止：

time_complexity.c
/* 指数阶（递归实现） */
int expRecur(int n) {
    if (n == 1)
        return 1;
    return expRecur(n - 1) + expRecur(n - 1) + 1;
}

指数阶增长非常迅速，在穷举法（暴力搜索、回溯等）中比较常见。对于数据规模较大的问题，指数阶是不可接受的，通常需要使用动态规划或贪心等算法来解决。

对数阶 \(O(\log n)\)

与指数阶相反，对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 \(n\) ，由于每轮缩减到一半，因此循环次数是 \(\log_2 n\) ，即 \(2^n\) 的反函数。

下图和以下代码模拟了“每轮缩减到一半”的过程，时间复杂度为 \(O(\log_2 n)\) ，简记为 \(O(\log n)\) 。

time_complexity.c
/* 对数阶（循环实现） */
int logarithmic(float n) {
    int count = 0;
    while (n > 1) {
        n = n / 2;
        count++;
    }
    return count;
}

对数阶的时间复杂度

与指数阶类似，对数阶也常出现于递归函数中。以下代码形成了一个高度为 \(\log_2 n\) 的递归树：

time_complexity.c
/* 对数阶（递归实现） */
int logRecur(float n) {
    if (n <= 1)
        return 0;
    return logRecur(n / 2) + 1;
}

对数阶常出现于基于分治策略的算法中，体现了“一分为多”和“化繁为简”的算法思想。它增长缓慢，是仅次于常数阶的理想的时间复杂度。

\(O(\log n)\) 的底数是多少？

准确来说，“一分为 \(m\)”对应的时间复杂度是 \(O(\log_m n)\) 。而通过对数换底公式，我们可以得到具有不同底数的、相等的时间复杂度：

\[ O(\log_m n) = O(\log_k n / \log_k m) = O(\log_k n) \]

也就是说，底数 \(m\) 可以在不影响复杂度的前提下转换。因此我们通常会省略底数 \(m\) ，将对数阶直接记为 \(O(\log n)\) 。

线性对数阶 \(O(n \log n)\)

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 \(O(\log n)\) 和 \(O(n)\) 。相关代码如下：

time_complexity.c
/* 线性对数阶 */
int linearLogRecur(float n) {
    if (n <= 1)
        return 1;
    int count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

下图展示了线性对数阶的生成方式。二叉树的每一层的操作总数都为 \(n\) ，树共有 \(\log_2 n + 1\) 层，因此时间复杂度为 \(O(n \log n)\) 。

线性对数阶的时间复杂度

主流排序算法的时间复杂度通常为 \(O(n \log n)\) ，例如快速排序、归并排序、堆排序等。

阶乘阶 \(O(n!)\)

阶乘阶对应数学上的“全排列”问题。给定 \(n\) 个互不重复的元素，求其所有可能的排列方案，方案数量为：

\[ n! = n \times (n - 1) \times (n - 2) \times \dots \times 2 \times 1 \]

阶乘通常使用递归实现。如下图和以下代码所示，第一层分裂出 \(n\) 个，第二层分裂出 \(n - 1\) 个，以此类推，直至第 \(n\) 层时停止分裂：

time_complexity.c
/* 阶乘阶（递归实现） */
int factorialRecur(int n) {
    if (n == 0)
        return 1;
    int count = 0;
    for (int i = 0; i < n; i++) {
        count += factorialRecur(n - 1);
    }
    return count;
}

阶乘阶的时间复杂度

请注意，因为当 \(n \geq 4\) 时恒有 \(n! > 2^n\) ，所以阶乘阶比指数阶增长得更快，在 \(n\) 较大时也是不可接受的。