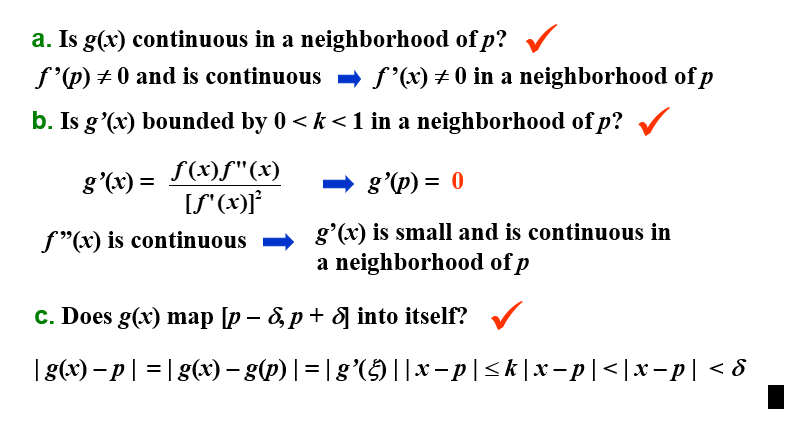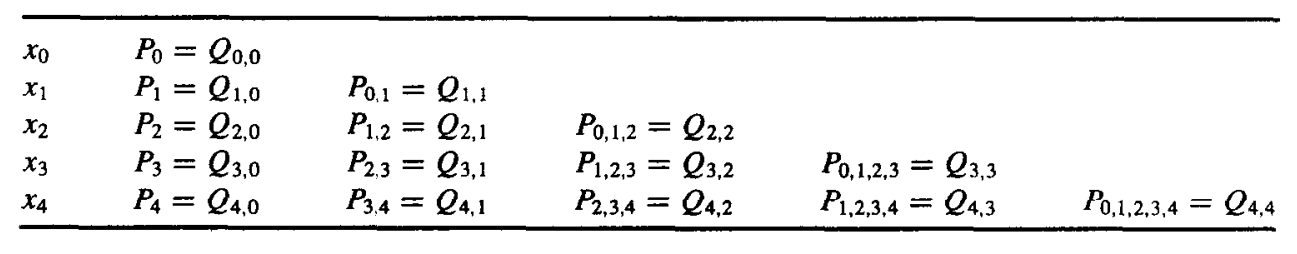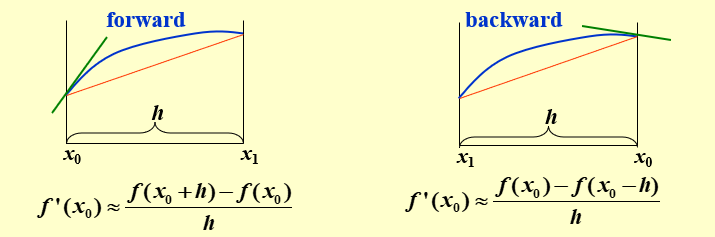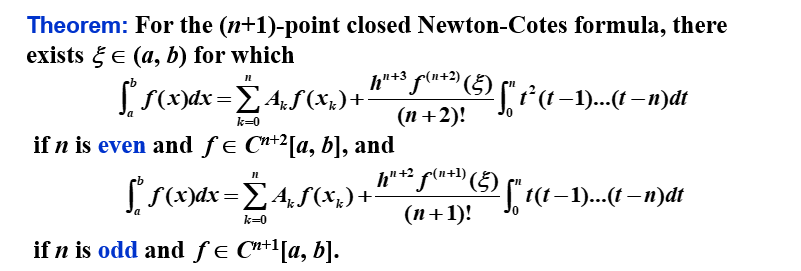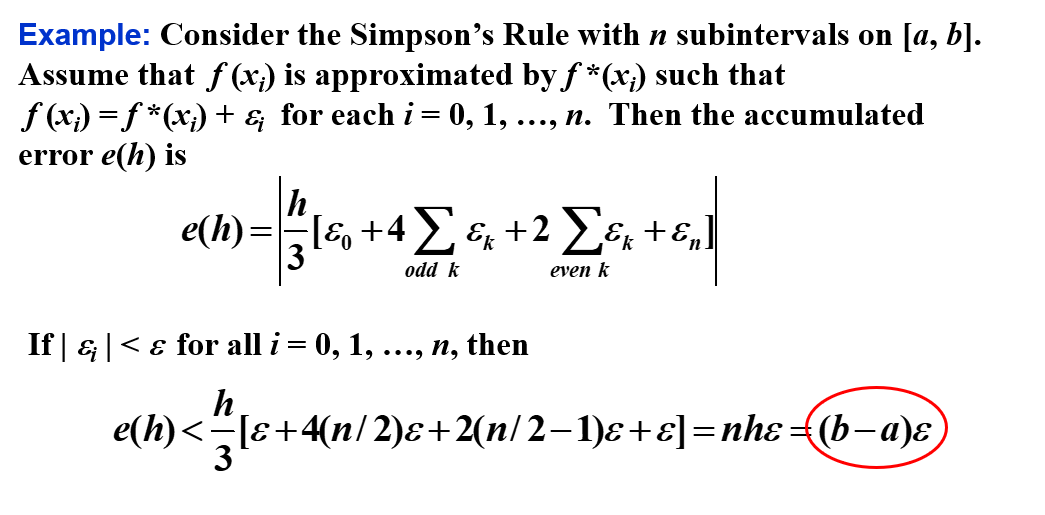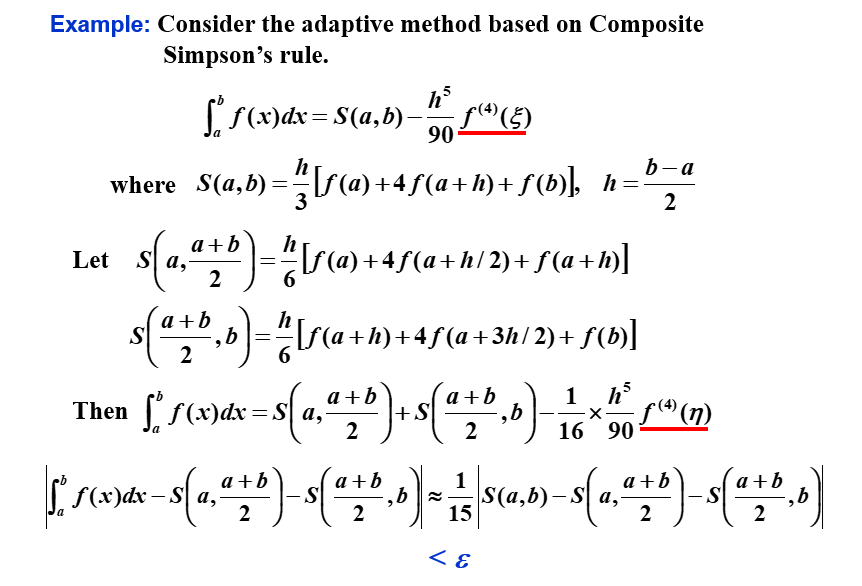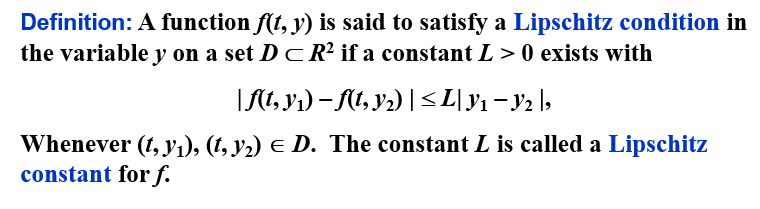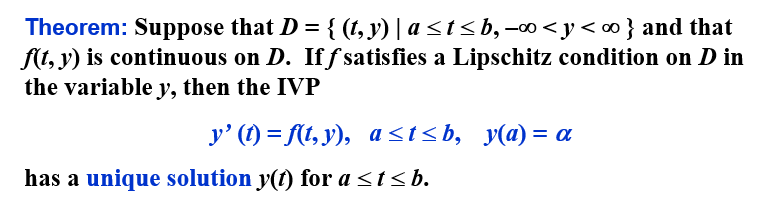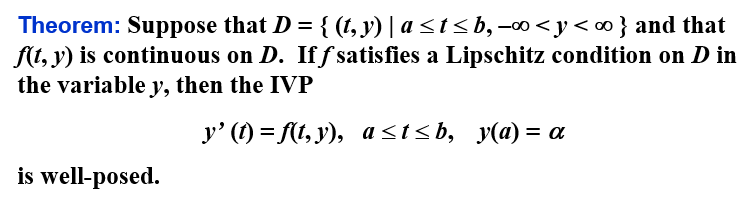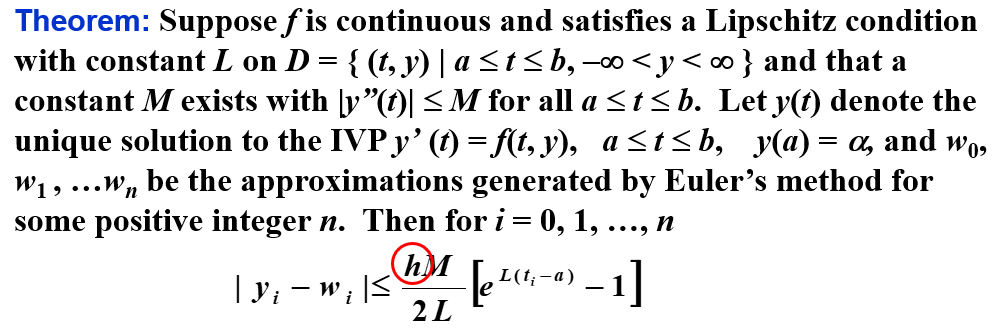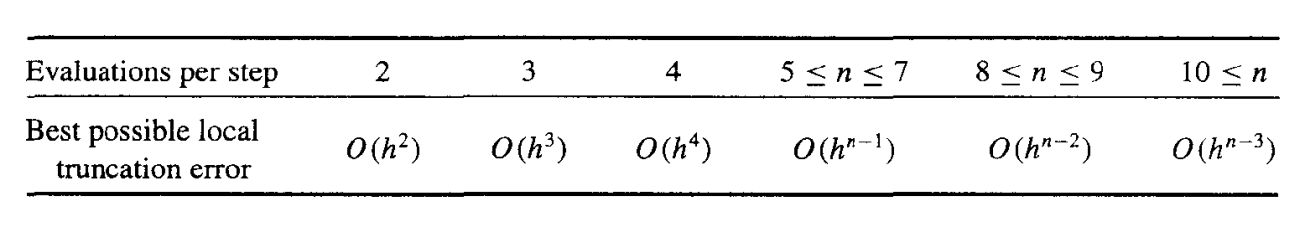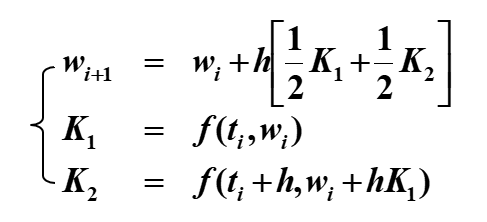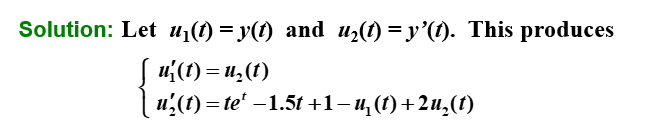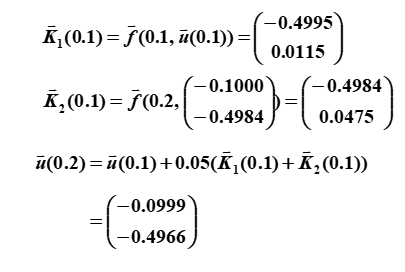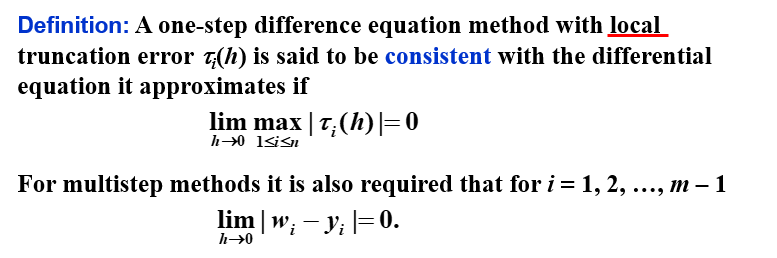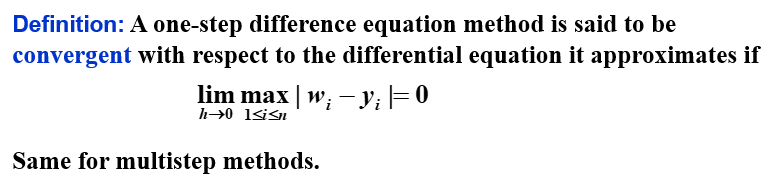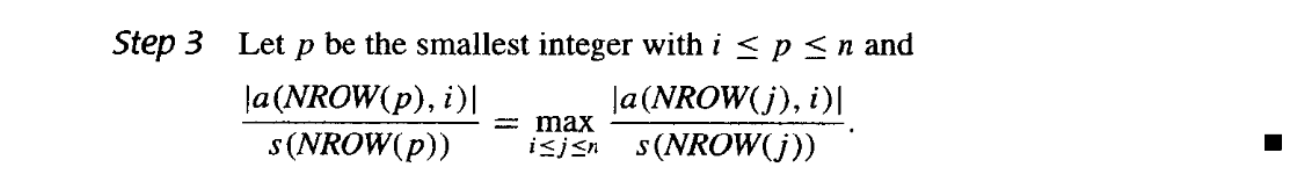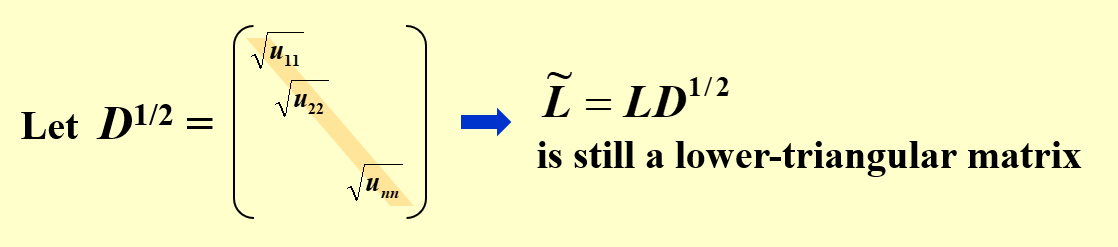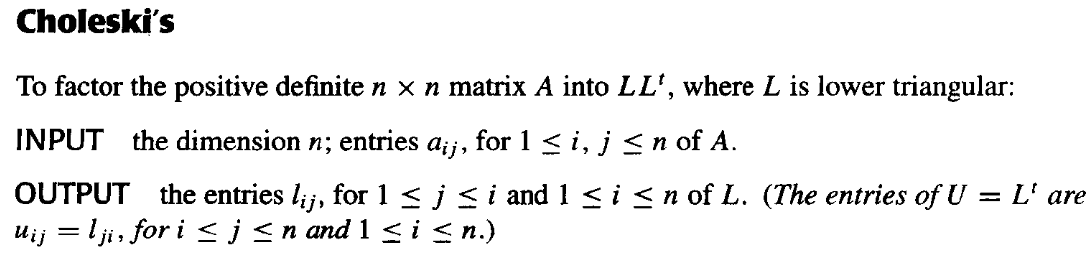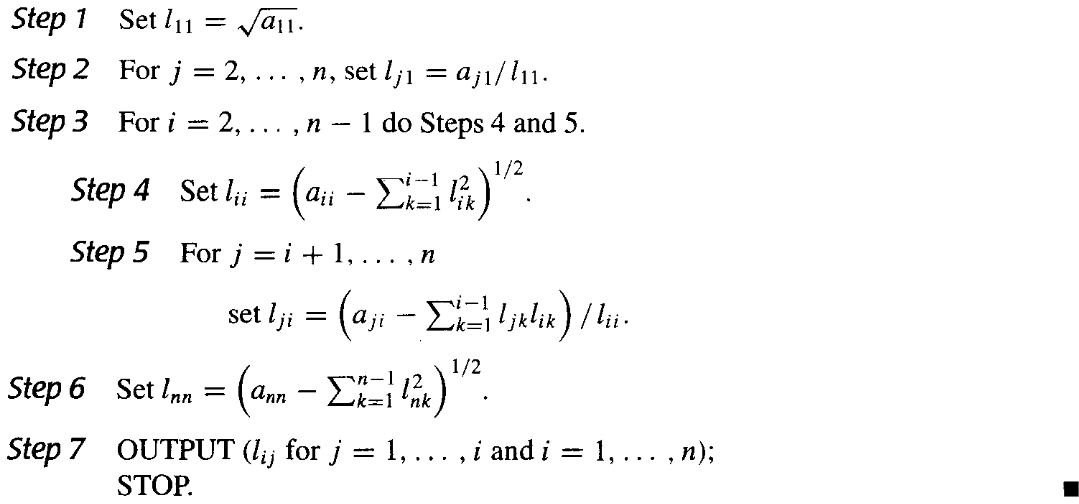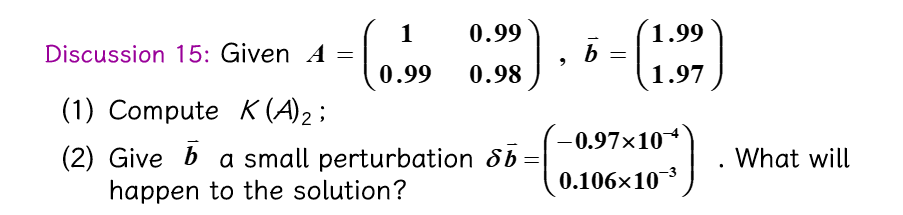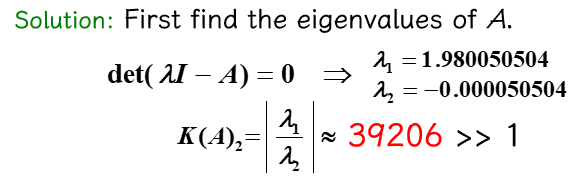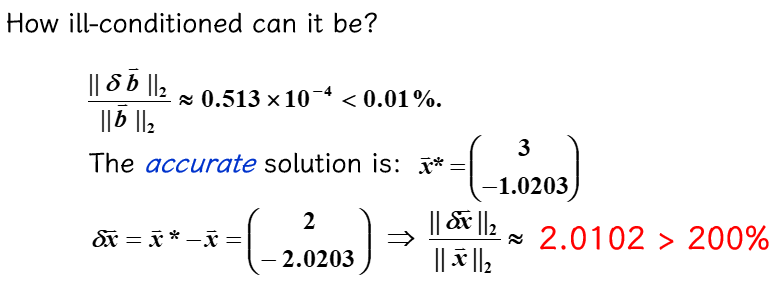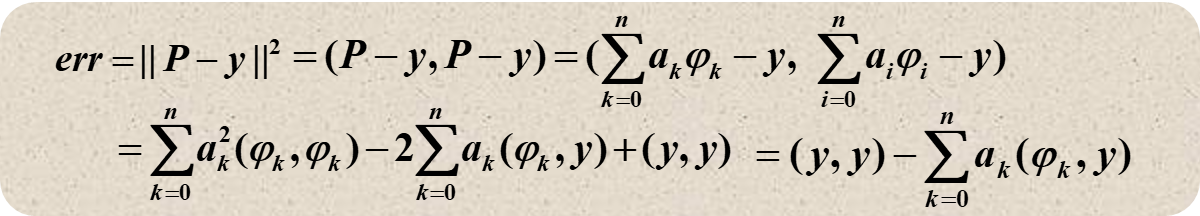数值分析
"课程架构"
"Interpolation and approximation"
Chapter 1 数学基础 | Mathematical Preliminaries
"本讲概述"
本讲主要介绍数值计算中的误差类型和误差分析,以及IEEE 754浮点数表示。
1.2 舍入误差和计算机算术 | Roundoff Errors and Computer Arithmetic
1.2.1 截断误差和舍入误差 | Truncation Error and Roundoff Error
1.2.2 截断法和舍入法 | Chopping and Rounding
使用舍入法或截断法产生的误差都叫做舍入误差。
- Chopping: 0.1119 -> 0.111,直接截断
- Rounding: 0.1119 -> 0.112,四舍五入
"函数表示"
Given a real number y=0.d1d2d3…dkdk+1…×10n(which is called Normalized decimal floating-point form of a real number)
fl(y)={0.d1d2d3…dk×10nchop(y+5×10n−(k+1))/* chopping *//* rounding */
1.2.3 绝对误差与相对误差 | Absolute error and relative error
Denote p∗ as the approximation of p.
- Absolute error: ∣p∗−p∣
- Relative error: ∣p∣∣p∗−p∣
"近似产生的误差"
chopping:
∣y∣∣y−fl(y)∣=0.d1d2d3…dk×10n0.dk+1dk+2…×10n−k=0.d1d2d3…dk0.dk+1dk+2…×10−k<0.11×10−k=10−k+1
Rounding:
∣y∣∣y−fl(y)∣≤0.d1d2d3…dk×10n0.5×10n−k=0.10.5×10−k=0.5×10−k+1
"误差产生"
- 两个近乎相等的数相减二导致有效数字的相消,例如:a=0.123456789,b=0.123456788,两者本来有9位有效数字,但是相减后只剩下1位有效数字。
- 如果有限位的表示或计算产生了误差,则除以一个小数(或者乘以一个大数)会放大绝对误差。
误差计算举例:
Evaluate f(x)=x3−6.1x2+3.2x+1.5 at x=4.71 using 3-digit arithmetic(3位有效数字).
|
x |
x2 |
x3 |
6.1x2 |
3.2x |
| exact |
4.71 |
22.1841 |
104.487111 |
135.32301 |
15.072 |
| Chopping |
4.71 |
22.1 |
104. |
6.1∗22.1=134.81≈134. |
15.0 |
| Rounding |
4.71 |
22.2 |
105. |
6.1∗22.2=135.42≈135. |
15.1 |
Exact value: f(4.71)=104.487111−135.32301+15.072+1.5=−14.263899
Chopping: f(4.71)=104−134+15.0+1.5=−13.5
- Relative error: ∣−14.263899∣∣−14.263899+13.5∣≈5.35%
Rounding: f(4.71)=105−135+15.1+1.5=−13.4
- Relative error: ∣−14.263899∣∣−14.263899+13.4∣≈6.06%
可见,有时候舍入误差比截断误差更大。
乘法较多会导致式子的误差较大,此时可以使用秦九韶算法(其实就是不断提取x)来减少乘法的次数。
把一个多项式f(x)=anxn+an−1xn−1+…+a1x+a0写成如下形式:
f(x)=((…(anx+an−1)x+an−2)x+…)x+a1)x+a0
然后从最内层开始计算。
将上例改写成秦九韶算法:
f(x)=((x−6.1)x+3.2)x+1.5
Chopping:
=====((4.71−6.1)4.71+3.2)4.71+1.5(−1.39∗4.71+3.2)4.71+1.5(−6.54+3.2)4.71+1.5−3.34∗4.71+1.5−15.7+1.5−14.2
Relative error: ∣−14.263899∣∣−14.263899+14.2∣≈0.44%
Rounding:
=====((4.71−6.1)4.71+3.2)4.71+1.5(−1.39∗4.71+3.2)4.71+1.5(−6.55+3.2)4.71+1.5−3.35∗4.71+1.5−15.8+1.5−14.3
Relative error: ∣−14.263899∣∣−14.263899+14.3∣≈0.25%
可见,此时误差明显减小了。
1.3 算法和收敛性 | Algorithms and Convergence
稳定性 | Stability
一个算法,如果初始数据的小变化会导致最终结果的小变化,则称为稳定(stable);否则称为不稳定(unstable)。
一个算法,如果只有在某些初始数据的选择下才是稳定的,则称为条件稳定(conditionally stable)。
误差增长 | The growth of errors
假设E0>0是初始误差(initial error),En是第n步的误差。
- 如果En≈CnE0,则称为线性增长(linear growth)。
线性增长的误差通常是无法避免的,当C和E0都很小的时候,结果通常是可以接受的。
- 如果En≈CnE0,则称为指数增长(exponential growth)。
指数增长的误差应该避免,因为即使E0很小,Cn也会变得很大。这会导致不可接受的不准确性。
收敛速度 | Convergence rate
使用O符号来表示收敛速度。
假设limh→0F(h)=L,limh→0G(h)=0。如果存在正常数K使得
∣F(h)−L∣≤K∣G(h)∣
对于足够小的h成立,则记为F(h)=L+O(G(h))
我们通常取G(h)=hp,(p>0),并对最大的p值感兴趣。
"求当h→0时下列函数的收敛速度"
F(h)=hsinh, limh→0hsinh=1
解: F(h)−L=hsinh−1=hsinh−h∼hh−6h3+o(h3)−h∼−6h2≤K∣h2∣
所以收敛速度为O(h2)。
1.4 IEEE 754 FLOATING POINT REPRESENTATION
二进制的科学计数法:x=±1.d1d2d3…dk×2n,这里的di是二进制的数字,1.d1d2d3…dk为有效位数(Significand)。
在计算机里有两种表示方法,分别是Single(32位)和double(64位)。均为下图的形式。

x=(−1)S×(1+Fraction)×2Exponent−Bias
- S代表符号位(sign bit)。S为0表示非负数,S为1表示负数。
- 有效位数(Significand=1+Fraction) 中1是默认的,我们只存储小数点后面的位数(即Fraction)。
- Fraction 代表尾数部分(也称作mantissa)。
- Single: 23 bits
- Double: 52 bits
- Exponent 表示指数部分(也称作characteristic)。
- Single: 8 bits
- Double: 11 bits
- excess representation(偏移表示法) = actual exponent − bias,其中:
- Single: bias=127 bits
- Double: bias=1023 bits
- 指数为全 0 和全 1 时用作特殊值处理
"Single & Double的值域"
"Single的值域"
-
最小值:
-
Exponent = 00000001, Fraction = 000...000
-
x=±(1+0.0)×21−127=±1.0×2−126≈±1.2×10−38
-
最大值:
-
Exponent = 11111110, Fraction = 111...111
-
x=±(1+0.111…111)×2254−127≈±2.0×2127≈±3.4×1038
"Double的值域"
-
最小值:
-
Exponent = 00000000001, Fraction = 000...000
-
x=±(1+0.0)×21−1023=±1.0×2−1022≈±2.2×10−308
-
最大值:
-
Exponent = 11111111110, Fraction = 111...111
-
x=±(1+0.111…111)×22046−1023≈±2.0×21023≈±1.8×10308
"Single & Double的十进制精度"
"Single的十进制精度"
- 最小分度: 2−23
- log102−23≈−6.92
- 所以约为小数点后六位有效数字
"Double的值域"
- 最小分度: 2−52
- log102−52≈−15.65
- 所以约为小数点后十六位有效数字
"十进制->IEEE754 浮点数"
"Represent –0.75"
- Convert to binary: 0.75=0.11
- Normalize: 0.11=1.1×2–1
- Sign bit: S=1
- Exponent:
- Single: –1+127=126=01111110
- Double: –1+1023=1022=01111111110
- Fraction:
- Single: 0.1=100⋯00,共23位
- Double: 0.1=100⋯00000,共52位
∴ IEEE 754 Representation:
- Single: 1 01111110 100⋯00
- Double: 1 01111111110 100⋯00000
"IEEE754 浮点数->十进制"
"What number is represented by the single-precision float 11000000101000…00"
- Sign bit: S=1
- Exponent: E=10000001=129
- Actual exponent: E−127=2
- Fraction: 01000⋯00
- Significand: 1.01000⋯00=1.25
- ∴ Number: –1.25×22=–5.0
Chapter 2 一元方程的求解 | Solutions of Equations in One Variable
2.0 停机程序 | Stopping procedure
我们可以选择一个精度要求ϵ,逐步迭代,直到满足下列条件之一:
- ∣xi+1−xi∣<ϵ
- ∣f(xi+1)∣<ϵ
- ∣xi+1∣∣xi+1−xi∣<ϵ
如果∣xi+1−xi∣收敛于0而序列本身发散 ,1号会失效。
也有可能f(x)与0很接近,但是xn与x差别很大,2号也不行了。
3号条件是能运用的最好的停机准则,因为它最接近测试相对误差。
2.1 二分法 | Bisection Method

"为什么要用a+(b-a)/2,而不用(b+a)/2?"
- 因为a和b可能是很大的数,相加可能会溢出。
- 因为a和b可能是很小的数,相加可能会产生舍入误差。用此方法可以确保a+(b-a)/2落在a和b之间。
- 例如,用截断保留2位有效数字,a=0.91,b=0.93,(a+b)/2=1.8/2=0.9,而a+(b-a)/2=0.91+(0.93-0.91)/2=0.92。
2.2 不动点迭代 | Fixed-Point Iteration

不动点的存在性和唯一性的充分条件:
a. g∈C[a,b]且g(x)∈[a,b],∀x∈[a,b],则g在[a,b]上有不动点。
b. ∣g′(x)∣≤k<1,∀x∈(a,b),则该不动点是唯一的。
则对于任意p0∈[a,b],不动点迭代序列pn+1=g(xn)收敛于不动点。
且我们有误差限∣pn−p∣≤1−kkn∣p1−p0∣,这将收敛速率和一阶导数的界联系起来。
"误差界分析"
∣pn+1−pn∣=∣g(pn)−g(pn−1)∣=∣g′(ξ)∣∣pn−pn−1∣≤k∣pn−pn−1∣≤k2∣pn−1−pn−2∣≤…≤kn∣p1−p0∣
∣pn−p∣=∣pn−pn−1+pn−1−pn−2+…+p1−p0∣≤∣pn−pn−1∣+∣pn−1−pn−2∣+…+∣p1−p0∣≤(kn−1+kn−2+…+1)∣p1−p0∣=k−1kn−1∣p1−p0∣≤1−kkn∣p1−p0∣
2.3 牛顿迭代法 | Newton's Method
就是用切线逼近零点,然后求切线与x轴的交点,作为下一个点,如此往复。
xn+1=xn−f′(xn)f(xn)

"定理:设f∈C2[a,b],如果p∈[a,b]满足f(p)=0且f′(p)=0,则存在δ>0,使得对任何初始值p0∈(p−δ,p+δ),牛顿迭代法产生收敛于p的序列{pn}n=1∞。"
证明:
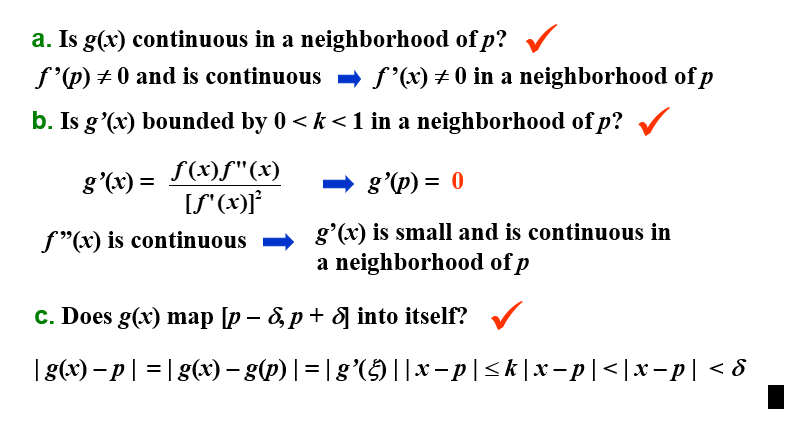
牛顿迭代法的收敛性取决于初始近似值的选择。
2.4 迭代法的误差分析 | Error Analysis for Iterative Methods
假设{pn}n=0∞收敛于p,其中对∀pn=p。如果存在正数λ和α,使得
n→∞lim∣pn−p∣α∣pn+1−p∣=λ
则称{pn}n=0∞是α阶收敛的(converges to p of order α),λ称为渐进误差常数(asymptotic error constant)。
一般具有高阶收敛性的序列收敛速度更快。
不动点法
不动点法的收敛阶和渐进误差常数:
pn+1−p=g(pn)−g(p)=g′(ξ)(pn−p)⇒∣pn−p∣∣pn+1−p∣=∣g′(ξ)∣⇒n→∞lim∣pn−p∣∣pn+1−p∣=n→∞lim∣g′(ξ)∣=∣g′(p)∣
因此,如果g′(p)=0,则不动点迭代法是线性收敛的,且渐进误差常数为∣g′(p)∣。
牛顿迭代法
牛顿迭代法的收敛阶和渐进误差常数:
由泰勒展开:
0=f(p)=f(pn)+f′(pn)(p−pn)+2f′′(ξ)(p−pn)2⇒p=pn−f′(pn)f(pn)−2f′(pn)f′′(ξ)(p−pn)2⇒n→∞lim∣pn−p∣2∣pn+1−p∣=n→∞lim2∣f′(pn)∣∣f′′(ξ)∣=2∣f′(p)∣∣f′′(p)∣
因此,牛顿迭代法是二次收敛的,且渐进误差常数为2∣f′(p)∣∣f′′(p)∣。
不动点法的多重根情况
如果p是g(x)的不动点,存在正整数m,使得g′(p)=g′′(p)=…=g(m−1)(p)=0,且g(m)(p)=0,则称pn=g(pn−1)以阶m收敛于p,渐进误差常数为m!∣g(m)(p)∣。
pn+1=g(pn)=g(p)+g′(p)(pn−p)+2g′′(ξ)(pn−p)2+…+m!g(m)(ξ)(pn−p)m⇒n→∞lim∣pn−p∣m∣pn+1−p∣=n→∞limm!∣g(m)(ξ)∣=m!∣g(m)(p)∣
牛顿法的多重根情况
如果p是f的m重零点,则有f(x)=(x−p)mq(x),记g(x)=x−f′(x)f(x),牛顿法即为 pn=g(pn−1)
g′(x)=1−(f′(x))2f′(x)2−f(x)f′′(x)=(f′(x))2f(x)f′′(x)=(m(x−p)m−1q(x)+q′(x)(x−p)m)2(x−p)mq(x)(m(m−1)(x−p)m−2q(x)+2m(x−p)m−1q′(x)+q′′(x)(x−p)m)=(x−p)2m−2(mq(x)+q′(x)(x−p))2(x−p)2m−2q(x)(m(m−1)q(x)+2m(x−p)q′(x)+q′′(x)(x−p)2)=(mq(x)+q′(x)(x−p))2q(x)(m(m−1)q(x)+2m(x−p)q′(x)+q′′(x)(x−p)2)
所以
g′(p)=(mq(p))2q(p)m(m−1)q(p)=1−m1<1
由不动点法的迭代情况可知,此时为线性收敛,不为二次收敛。
牛顿法多重根下的优化
定义
μ(x)=f′(x)f(x)
如果p是f 的m重零点,f(x)=(x−p)mq(x),则
μ(x)=m(x−p)m−1q(x)+q′(x)(x−p)m(x−p)mq(x)=mq(x)+q′(x)(x−p)(x−p)q(x)
又q(p)=0,且
mq(p)+q′(p)(p−p)q(p)=m1=0
所以p是μ(x)的单根,那么我们对μ应用牛顿迭代法,就有
pn+1=g(pn)=pn−μ′(pn)μ(pn)=pn−(f′(pn))2f′(pn)f′(pn)−f(pn)f′′(pn)f′(pn)f(pn)=pn−f′(pn)2−f(pn)f′′(pn)f(pn)f′(pn)
这就是让有多重根的牛顿法二次收敛的方法。
- 要求二阶导
- 分母由两个接近于0的数相减,会引起严重的舍入误差。
2.5 加速收敛 | Accelerating Convergence
二次收敛是很少可以得到的,我们在日常中总会碰到线性收敛。为了考虑如何加速线性收敛序列的收敛速度,下面介绍——AITKENΔ2方法。
AITKENΔ2方法
"Δ"
对于给定的序列,向前差分(forward difference)定义为Δpn=pn+1−pn,对于更高的幂,我们有Δkpn=Δ(Δk−1pn),比如Δ2pn=Δ(Δpn)=Δ(pn+1−pn)=(pn+2−pn+1)−(pn+1−pn)
假设{pn}n=0∞是线性收敛的,其极限为p。
为了便于构造比{pn}n=0∞收敛更快的序列{p^n}n=0∞,我们假设pn−p,pn+1−p,pn+2−p的符号一致,又假设n足够大,有
pn−ppn+1−p≈pn+1−ppn+2−p
从而
pn+12−2pn+1p+p2≈pn+2pn−(pn+pn+2)p+p2
解出p,得到
p≈pn+2−2pn+1+pnpn+2pn−pn+12≈pn−pn+2−2pn+1+pn(pn+1−pn)2
于是,我们可以构造序列{p^n}n=0∞,其中
p^n=pn−pn+2−2pn+1+pn(pn+1−pn)2=pn−Δ2pn(Δpn)2
这样定义序列的方法就是AITKENΔ2法
"为什么说更快?"
可以证明
n→∞limpn−ppn^−p=0
"怎么迭代?"
其实还是用序列本身的迭代法,不过在计算值的时候采取了AITKENΔ2法。
构造按如下顺序:
p0,p1=g(p0),p2=g(p1)p0^={Δ2}(p0)p3=g(p2)p1^={Δ2}(p1)⋮
Steffensen 方法
这个方法假设p0^比p2更好地逼近p,从而把上述过程第三行的不动点迭代应用到p0^上
p0(0),p1(0)=g(p0(0)),p2(0)=g(p1(0))p0(1)={Δ2}(p0(0))p1(1)=g(p0(0))⋮
算法如下:

注意Δ2pn可能为0,如果发生,则终止并选取p2(n−1)为近似解。
我们一般要求g′(p)=0,则在邻域内Steffensen法是二次收敛的
Chapter 3 插值和多项式逼近 | Interpolation and Polynomial Approximation
3.1 插值和 Lagrange 多项式 | Interpolation and Lagrange Polynomials
构造 Lagrange 多项式
拉格朗日插值就是构造一个次数至多为 n 次的多项式使它通过 n+1 个给定的点,这个多项式就是拉格朗日多项式。
" n=1 "
构造P(x)=a0+a1x,使得P(x0)=y0,P(x1)=y1。
则P(x)=y0+x1−x0y1−y0(x−x0)=x0−x1x−x1y0+x1−x0x−x0y1。
其中x0−x1x−x1和x1−x0x−x0分别记作L1,0(x)和L1,1(x)(第一个下标即为n的值,第二个下标为样本点的序号),这称为拉格朗日基函数(Lagrange Basis)。
可以知道,拉格朗日基函数总是满足Kronecker Delta函数δij。
δij={1,0,i=ji=j
推广到n次插值,构造P(x)=a0+a1x+⋯+anxn,使得P(xi)=yi,i=0,1,⋯,n。就是要找到 Ln,i(x) 使得 Ln,i(xj)=δij
分析可知,这里的Ln,i(x)有 n 个根,分别为x0,x1,⋯,xi−1,xi+1,⋯,xn。所以可以构造出
Ln,i(x)=C(x−x0)(x−x1)⋯(x−xi−1)(x−xi+1)⋯(x−xn)
又因为Ln,i(xi)=1,所以
Ln,i(x)=(xi−x0)(xi−x1)⋯(xi−xi−1)(xi−xi+1)⋯(xi−xn)(x−x0)(x−x1)⋯(x−xi−1)(x−xi+1)⋯(x−xn)
即
Ln,i(x)=j=0,j=i∏nxi−xjx−xj
于是我们根据拉格朗日基函数构造出了 n 次拉格朗日插值多项式
Pn(x)=i=0∑nLn,i(x)yi
Lagrange 多项式的唯一性
对 n 个不同的点 , n 次拉格朗日插值多项式是唯一的
证明:
如果不唯一,假设存在另一个多项式Qn(x),使得Qn(xi)=yi,i=0,1,⋯,n,且Qn(x)=Pn(x)。
则Rn(x)=Pn(x)−Qn(x)是一个次数不超过n的多项式,且Rn(xi)=0,i=0,1,⋯,n。
由于Rn(x)的次数不超过n,n次多项式不可能有 n+1 个解,所以Rn(x)=0,即Pn(x)=Qn(x),与假设矛盾。
如果 对 n 个点 运用 超过n 次的拉格朗日插值多项式,那么得到的多项式就不唯一了。
例如 P(x)=Ln(x)+p(x)i=0∏n(x−xi)
拉格朗日逼近的余项
假定a≤x0<x1<⋯<xn≤b,f∈C[a,b],Pn(x)是f(x)在x0,x1,⋯,xn上的拉格朗日插值多项式,则对任意x∈[a,b],存在ξ(x)∈(a,b),使得
f(x)−Pn(x)=(n+1)!f(n+1)(ξ(x))i=0∏n(x−xi)
"证明"
记Rn(x)=f(x)−Pn(x),则Rn(x)是一个次数不超过n的多项式,且Rn(xi)=0,i=0,1,⋯,n。所以Rn(x)可记作C(x)i=0∏n(x−xi)
固定一个点x (x=xi) 时,记g(t)=Rn(t)−C(x)i=0∏n(t−xi),则g(x)=0,g(xi)=0,i=0,1,⋯,n,所以g(t)存在n+2个不同的零点
根据推广的Rolle定理,存在ξ(x)∈(a,b),使得g(n+1)(ξ(x))=0,即
0=g(n+1)(ξ(x))=(Rn(ξ(x))−C(x)i=0∏n(ξ(x)−xi))(n+1)=(f(ξ(x))−Pn(ξ(x))−C(x)i=0∏n(t−xi))(n+1)=f(n+1)(ξ(x))−C(x)(n+1)!//因为Pn(x)是n次多项式,所以Pn(n+1)(x)=0
所以C(x)=(n+1)!f(n+1)(ξ(x)),所以Rn(x)=(n+1)!f(n+1)(ξ(x))i=0∏n(x−xi)
因为这里的f(n+1)(ξ(x))是不知道的,所以我们经常用f(n+1)(x)的上界来估计余项。
分析余项可知,对于小于等于 n 次的多项式 f ,经过n次拉格朗日插值得到的余项为0,得到的多项式就是 f 本身
例子 1
假设为 x∈[0,1] 的函数 f(x)=ex 做一个表格。设表中每一项精确的位数是 d≥8,相邻 x 值之差即步长为 h。为使线性插值(即一次Lagrange插值)的误差不超过 10−6,h应该是多少?
解:
假设 [0,1] 被分成 n 个等距的子区间 [x0,x1],[x1,x2],⋯,[xn−1,xn],x 在区间 [xk,xk+1] 中。则误差估计为
∣f(x)−P1(x)∣=∣2!f′′(ξ(x))(x−xk)(x−xk+1)∣≤∣2eξ(x−kh)(x−(k+1)h)∣≤2e⋅4h2≤10−6
所以 h≤1.72×10−3。我们不妨取 h=10−3,则 n=1000。
例子 2

给三个点,我们有两种方法来线性插值。往往,内插(Intrapolation) 会比 外插(Extrapolation) 更加准确。

高次的拉格朗日插值一般会比低次的插值更加准确,但是这不一定总成立。
Neville 迭代插值法
记号说明: 设 f 在 x0,x1,⋯,xn 上有定义,m1,m2,⋯,mk 是 k 个不同的整数,0≤mi≤n,i=1,2,⋯,k。记在这 k 个点上与 f(x) 相同的拉格朗日多项式为 Pm1,m2,⋯,mk(x)。
定理: 设 f 在 x0,x1,⋯,xn 上有定义,让 xi 和 xj 是这个集合中的两个不同的数。则
P(x)=(xi−xj)(x−xj)P0,1,...,j−1,j+1,...,k(x)−(x−xi)P0,1,...,i−1,i+1,...,k(x)
描述了对 f 在 x0,x1,⋯,xk 这 k+1个点 上的 k 次插值多项式。
"五个点"
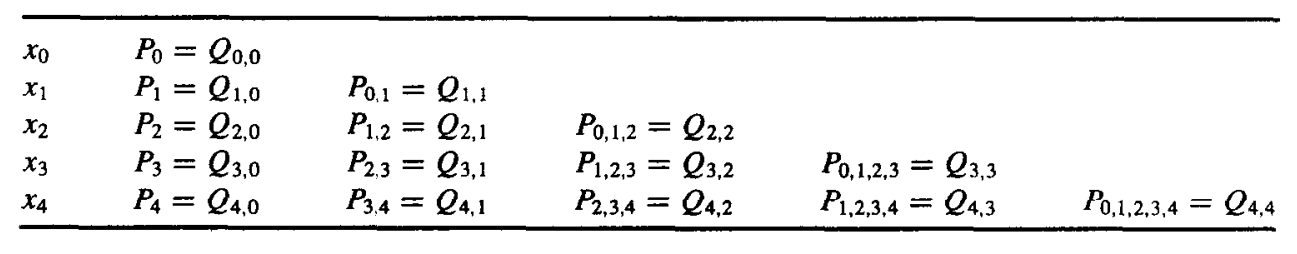
证明:
对于任意 0≤r≤k,r=i 和 r=j,分子上的两个插值多项式在 xr 处都等于 f(xr),所以 P(xr)=f(xr)。
分子上的第一个多项式在 xi 处等于 f(xi),而第二个多项式在 xi 处为0,所以 P(xi)=f(xi)。同理 P(xj)=f(xj)。
所以 P(x) 在 x0,x1,⋯,xk 上与 f(x) 相同,因为 P(x) 是 k 次多项式,所以 P(x)=P0,1,⋯,k(x)。
伪代码

3.2 Divided Differences | 差商
设 Pn(x) 是函数 f 在点 x0,x1,⋯,xn 上的拉格朗日多项式,f 关于 x0,x1,⋯,xn 的差商被用于将 Pn(x) 表示为:
Pn(x)=f[x0]+f[x0,x1](x−x0)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)
其中 f[x0,x1,⋯,xn] 是 f 关于 x0,x1,⋯,xn 的差商,通过代值可以得到
f[x0]=f(x0),f[x0,x1]=x1−x0f(x1)−f(x2),f[x0,x1,x2]=x2−x0f[x1,x2]−f[x0,x1],⋯
f[x0,x1,⋯,xn]=xn−x0f[x1,x2,⋯,xn]−f[x0,x1,⋯,xn−1]
我们记 f[x0],f[x0,x1],⋯,f[x0,x1,⋯,xn] 为 f 关于 x0,x1,⋯,xn 的 0 阶差商,1 阶差商,⋯,n 阶差商。
"六个点的三阶差商计算的例子"

同时,我们称
Pn(x)=f[x0]+f[x0,x1](x−x0)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)
为差商型 Newton 插值多项式(Newton's Interpolatory Divided-Difference formula)。
伪代码

差商和导数的关系
一阶差分
将中值定理应用到 f 在 [x0,x1] 上,得到
f[x0,x1]=x1−x0f(x1)−f(x0)=f′(ξ)
n 阶差分
设 f∈Cn[a,b] 且 x0,x1,⋯,xn∈[a,b],则存在 ξ∈(a,b),使得
f[x0,x1,⋯,xn]=n!f(n)(ξ)
证明:
设 g(t)=f(t)−Pn(t),则 g(xi)=0,i=0,1,⋯,n。所以 g(t) 在 [x0,xn] 上有 n+1 个零点,根据推广的 Rolle 定理,存在 ξ∈(a,b),使得 g(n)(ξ)=0,即
f(n)(ξ)−Pn(n)(ξ)=0
所以 Pn(n)(ξ)=f(n)(ξ),因为
Pn(n)(ξ)=n!f[x0,x1,⋯,xn]
所以
f[x0,x1,⋯,xn]=n!f(n)(ξ)
"PPT上采用的证明方法"

差分记号引入
如果每个点都连续等步长排列,记步长为h,令xi=x0+ih,则
引入**向前差分(forward difference)**记号:
Δf(xi)Δ2f(xi)Δ3f(xi)⋯=f(xi+1)−f(xi)=Δf(xi+1)−Δf(xi)=Δ2f(xi+1)−Δ2f(xi)
引入**向后差分(backward difference)**记号:
∇f(xi)∇2f(xi)∇3f(xi)⋯=f(xi)−f(xi−1)=∇f(xi)−∇f(xi−1)=∇2f(xi)−∇2f(xi−1)
引入**中心差分(central difference)**记号:
δkfi=δk−1fi+21−δk−1fi−21
其中
fi±21=f(xi±2h)
等距下的向前差商公式
在等距情况下,向前差商的公式可表示为:
Pn(xs)=Pn(x0+sh)=f[x0]+f[x0,x1]sh+⋯+f[x0,x1,⋯,xn]s(s−1)⋯(s−n+1)hn=k=0∑n(sk)k!hkf[x0,x1,⋯,xk]
这里的 (sk) 是组合数,即 k!s(s−1)⋯(s−k+1)
等距下的向前差分公式
由向前差分的记号可知道
f[x0,x1]f[x0,x1,x2]=x1−x0f(x1)−f(x0)=h1Δf(x0)=2h1[hΔf(x1)−Δf(x0)]=2h21Δ2f(x0),
由此可推广得出
f[x0,x1,…,xk]=k!hk1Δkf(x0).
所以
Pn(xs)=k=0∑n(sk)Δkf(x0)
此即为向前差分的公式
等距下的向后差商公式
重排插值节点再计算,此时:
Pn(x)=f[xn]+f[xn,xn−1](x−xn)+f[xn,xn−1,xn−2](x−xn)(x−xn−1)+⋯+f[xn,…,x0](x−xn)(x−xn−1)⋯(x−x1).
在等距情况下,记 xs=xn+sh=xi+(s+n−i)h,有
Pn(xs)===Pn(xn+sh)f[xn]+shf[xn,xn−1]+s(s+1)h2f[xn,xn−1,xn−2]+⋯+s(s+1)⋯(s+n−1)hnf[xn,…,x0]k=0∑n(−1)k(−sk)k!hkf[xn,xn−1,⋯,xn−k]
这里的 (−sk) 是组合数,即 k!−s(−s−1)⋯(−s−k+1)=(−1)k⋅k!s(s+1)⋯(s+k−1)
等距下的向后差分公式
由向后差分的记号可知道
f[xn,xn−1]f[xn,xn−1,xn−2]=h1∇f(xn),=2h21∇2f(xn),
由此可推广得出
f[xn,xn−1,…,xn−k]=k!hk1∇kf(xn).
所以
Pn(xs)=k=0∑n(−1)k(−sk)∇kf(xn)
3.3 Hermite Interpolation | Hermite 插值
Hermite 插值的目标是找到一个插值多项式
Osculating polynomials | 密切多项式
在 x0,x1,⋯,xn 上逼近 f∈Cm[a,b] 的密切多项式(osculating polynomial) 是具有以下性质的多项式 Pn(x):
- Pn(x) 在 x0,x1,⋯,xn 上与 f(x) 相同
- 对每个 xi,Pn(x) 和 f(x) 在 xi 处的前 mi 阶导数相同
- 因此,我们可以得到 i=0∑n(mi+1)=i=0∑nmi+(n+1) 个条件,于是 Pn(x) 是一个次数至多为 i=0∑nmi+n 的多项式
我们给出密切多项式的定义:
定义: 设 x0,x1,⋯,xn 是 [a,b] 上的 n+1 个不同的点,m0,m1,⋯,mn 是 n+1 个非负整数,假设f∈Cm[a,b],其中 m=0≤i≤nmaxmi。逼近 f 的密切多项式 Pn(x) 是使得下式成立的最小次数的多项式:
dxkdkPn(xi)=dxkdkf(xi),k=0,1,⋯,mi,i=0,1,⋯,n
- 当 n=0 时,逼近 f 的密切多项式是 f 在 x0 处的 m0 阶 Taylor 多项式。
- 当 mi=0 时,密切多项式就是对 f 在 x0,x1,⋯,xn 上插值的 n 次拉格朗日插值多项式。
Hermite 插值多项式
对密切多项式 mi=1 的情况,我们定义其为 Hermite 多项式。也就是说,多项式 P(n) 和它的一阶导数 P′(n) 在 xi 处与 f 和 f′ 相同。
特殊例子
假设 x0=x1=x2,给定 f(x0),f(x1),f(x2),f′(x1),找到多项式使得P(xi)=f(xi),P′(x1)=f′(x1)。
首先,其次数为3次,我们猜想其形式为
P(x)=i=0∑2f(xi)hi(x)+f′(x1)h^1(x)
其中hi(xj)=δi(xj),hi′(x1)=0,h^1(xi)=0,h^1′(x1)=1。
根据这个猜想,我们试图构造出 hi(x) 和 h^1(x) 。
首先,我们可以用拉格朗日同样的方法构造出三次多项式hi(x),使得hi(xj)=δi(xj),hi′(x1)=0,i=0,1,2。
对于h0(x),有根x1,x2,且因为 h0′(x1)=0 所以 x1 是 h0(x) 的二重根,所以其形式为
h0(x)=C0(x−x1)2(x−x2)
又因为h0′(x0)=1,所以
h0(x)=(x0−x1)2(x0−x2)(x−x1)2(x−x2)
类似地,我们可以得到
h2(x)=(x2−x0)(x2−x1)2(x−x0)(x−x1)2
对于h1(x),有根x0,x2,都是单根。所以其形式为
h1(x)=(Ax+B)(x−x0)(x−x2)
通过计算 h1(x1)=1,h1′(x1)=0,可以得到 A 和 B 的值。此处略。
然后,我们构造h^1(x),使得h^1(xi)=0,h^1′(x1)=1。对于h^1(x),有根x0,x1,x2,所以
h^1(x)=C(x−x0)(x−x1)(x−x2)
又因为h^1′(x1)=1,所以可以通过计算得到 C 的值。此处略。
一般情况
如果已知 f(x0),f(x1),⋯,f(xn) 和 f′(x0),f′(x1),⋯,f′(xn),则可以构造出 Hermite 插值多项式
H2n+1(x)=i=0∑nf(xi)hi(x)+i=0∑nf′(xi)h^i(x)
其中(2n+1)阶多项式hi(xj)=δi(xj),hi′(xj)=0,h^i(xj)=0,h^i′(xj)=δi(xj)。
对于hi(x),有根x0,x1,⋯,xi−1,xi+1,⋯,xn,且因为 hi′(xj)=0(j=i) 所以 xj 是 hi(x) 的 2 重根,所以其形式为
hi(x)=(A′x+B′)(x−x0)2(x−x1)2⋯(x−xi−1)2(x−xi+1)2⋯(x−xn)2=(Ax+B)Ln,i2(x)
这里的常系数改变是因为引入 Ln,i(x) 的话,它相较前面的有额外系数
Ln,i(x)=j=0,j=i∏nxi−xjx−xj
因为hi(xi)=1,hi′(xi)=0,所以
hi(x)=(1−2(x−xi)Ln,i′(xi))(Ln,i(x))2
对于h^i(x),有根x0,x1,⋯,xn,且因为 h^i′(xj)=0(j=i),h^i′(xi)=1 所以 xi 是 h^i(x) 的 1 重根,其余的都是 2 重根,所以其形式为
h^i(x)=Ci(x−xi)(Ln,i(x))2
因为h^i′(xi)=1,所以
h^i(x)=(x−xi)(Ln,i(x))2
余项
如果 a=x0<x1<⋯<xn=b,f∈C2n[a,b],余项为
f(x)−Pn(x)=(2n+2)!f(2n+2)(ξ(x))i=0∏n(x−xi)2
3.4 Cubic Spline Interpolation | 三次样条插值
Piecewise-polynomial approximation | 分段多项式逼近
最简单的分段多项式逼近是分段线性逼近,即在每个子区间上用一个一次多项式逼近函数 f。但是,分段线性逼近的函数不光滑,所以我们希望用更高次的多项式来逼近 f。
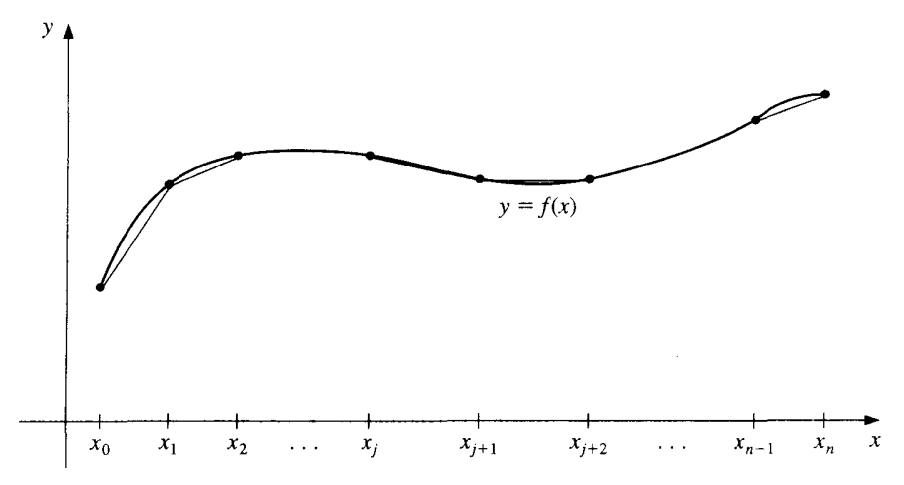
一个可替代的方法是使用 Hermite 插值多项式。例如,如果 f 和 f′ 的值在每一个点 xi 处都已知,那么我们可以在每个子区间上使用一个三次多项式来逼近 f。这样的逼近是光滑的,但是为了将该多项式应用于一般插值,需要知道所有的 f′ 的值,这是不现实的。
由此,我们引入了三次样条插值。
Cubic spline interpolation | 三次样条插值
三次样条的构造不假设插值函数的导数值与原函数的导数值相等,即使在插值点处也如此。
给定在 [a,b] 上的 n+1 个点 x0,x1,⋯,xn,a=x0<x1<⋯<xn=b,以及 f。三次样条插值是一个函数 S(x),满足以下条件:
- S(x) 在每个子区间 [xi,xi+1] 上是一个三次多项式,i=0,1,⋯,n−1
- S(xi)=f(xi),i=0,1,⋯,n
- Si+1(xi+1)=Si(xi+1),i=0,1,⋯,n−2
- Si+1′(xi+1)=Si′(xi+1),i=0,1,⋯,n−2
- Si+1′′(xi+1)=Si′′(xi+1),i=0,1,⋯,n−2
- 下列的边界条件之一成立:
- S′′(x0)=S′′(xn)=0,称为自由或自然边界(free or natural boundary)
- S′(x0)=f′(x0),S′(xn)=f′(xn),称为固支边界(clamped boundary)
- 其他边界条件(上面两个条件其实已经足以满足目的了)
我们介绍一种构造三次样条插值的方法:
Method of Bending Moments
记 hj=xj−xj−1,在 x∈[xj−1,xj] 上,S(x)=Sj(x),S′(x)=Sj′(x),S′′(x)=Sj′′(x)。
因为 S(x) 是一个三次多项式,所以 Sj′′(x) 是一个一次多项式,由端点值决定,假设 Sj′′(xj−1)=Mj−1,Sj′′(xj)=Mj。那么对于 x∈[xj−1,xj],有
Sj′′(x)=Mj−1hjxj−x+Mjhjx−xj−1
积分得到
Sj′(x)=−Mj−12hj(xj−x)2+Mj2hj(x−xj−1)2+Aj
再积分得到
Sj(x)=Mj−16hj(xj−x)3+Mj6hj(x−xj−1)3+Ajx+Bj
Aj 和 Bj 是常数,可以通过 Sj(xj−1)=yj−1 和 Sj(xj)=yj 得到。
{Sj(xj−1)=yj−1Sj(xj)=yj⇒{Mj−16hj2+Ajxj−1+Bj=yj−1Mj6hj2+Ajxj+Bj=yj⇒{Aj=hjyj−yj−1−6Mj−Mj−1hjBj=hjyj−1xj−yjxj−1−6Mj−1xj−Mjxj−1hj
所以
Ajx+Bj=hjyj−yj−1x+hjyj−1xj−yjxj−1−6Mj−Mj−1hjx−6Mj−1xj−Mjxj−1hj=(yj−1−6Mj−1hj2)hjxj−x+(yj−6Mjhj2)hjx−xj−1
所以,我们的目的就是求出 Mj,j=0,1,⋯,n。
因为 S′ 是连续的,所以
在 [xj−1,xj] 上,Sj′(x)=−Mj−12hj(xj−x)2+Mj2hj(x−xj−1)2+f[xj−1,xj]−6Mj−Mj−1hj
在 [xj,xj+1] 上,Sj+1′(x)=−Mj2hj+1(xj+1−x)2+Mj+12hj+1(x−xj)2+f[xj,xj+1]−6Mj+1−Mjhj+1
有 Sj+1′(xj)=Sj′(xj),所以我们可以得到 Mj−1,Mj,Mj+1 之间的关系:
记 λj=hj+hj+1hj+1,μj=hj+hj+1hj,gj=hj+hj+16(f[xj,xj+1]−f[xj−1,xj]),则
μjMj−1+2Mj+λjMj+1=gj
其中 j=1,2,⋯,n−1。
μ12μ2λ12⋱λ2⋱μn−1⋱2λn−1M0M1⋮Mn=g1g2⋮gn−1
我们有 n+1 个未知数,n−1个方程 → 由边界条件增加两个方程
Clamped boundary | 固支边界
此时我们知道 S′(x0)=f′(x0),S′(xn)=f′(xn),所以
在 [x0,x1] 上,S1′(x)=−M02h1(x1−x)2+M12h1(x−x0)2+f[x0,x1]−6M1−M0h1
在 [xn−1,xn] 上,Sn′(x)=−Mn−12hn(xn−x)2+Mn2hn(x−xn−1)2+f[xn−1,xn]−6Mn−Mn−1hn
所以我们额外有两个方程:
{f′(x0)=−M02h1+f[x0,x1]−6M1−M0h1f′(xn)=Mn2hn+f[xn−1,xn]−6Mn−Mn−1hn⇒{2M0+M1=h16(f[x0,x1]−f′(x0))≜g0Mn−1+2Mn=hn6(f′(xn)−f[xn−1,xn])≜gn
所以我们可以得到
2μ112⋱λ1⋱μn−1⋱21λn−12M0M1⋮Mn=g0g1⋮gn
Natural boundary | 自由边界
根据之前的假设,有 M0=S′′(x0)=y0′′,Mn=S′′(xn)=yn′′,则
λ0=0,g0=2y0′′,μn=0,gn=2yn′′
当 S′′(x0)=S′′(xn)=0,我们称之为自由边界(free boundary),此时 g0=gn=0。
2μ102⋱0λ1⋱μn−10⋱20λn−12(n+1)×(n+1)M0M1⋮Mn−1Mn(n+1)×1=g0g1⋮gn−1gn(n+1)×1
自由边界的情况下,有 S′′(x0)=S′′(xn)=0。
书上的方法
我们介绍另一种构造三次样条插值的方法:
给定在 [a,b] 上的 n+1 个点 x0,x1,⋯,xn,a=x0<x1<⋯<xn=b,设三次多项式 Sj(x) 为
Sj(x)=aj+bj(x−xj)+cj(x−xj)2+dj(x−xj)3,j=0,1,⋯,n−1
且满足
- S(x) 在每个子区间 [xi,xi+1] 上是一个三次多项式,i=0,1,⋯,n−1
- S(xi)=f(xi),i=0,1,⋯,n
- Si+1(xi+1)=Si(xi+1),i=0,1,⋯,n−2
- Si+1′(xi+1)=Si′(xi+1),i=0,1,⋯,n−2
- Si+1′′(xi+1)=Si′′(xi+1),i=0,1,⋯,n−2
- 下列的边界条件之一成立:
- S′′(x0)=S′′(xn)=0,称为自由或自然边界(free or natural boundary)
- S′(x0)=f′(x0),S′(xn)=f′(xn),称为固支边界(clamped boundary)
- 其他边界条件(上面两个条件其实已经足以满足目的了)
记 hj=xj−xj−1,由条件3,可得
aj+1=Sj+1(xj+1)=Sj(xj+1)=aj+bjhj+cjhj2+djhj3,j=0,1,⋯,n−1
又由条件4,因为 S′(x)=bj+2cj(x−xj)+3dj(x−xj)2,所以
bj+1=Sj+1′(xj+1)=Sj′(xj+1)=bj+2cjhj+3djhj2,j=0,1,⋯,n−1
又由条件5,因为 S′′(x)=2cj+6dj(x−xj),所以
cj+1=2Sj+1′′(xj+1)=cj+3djhj,j=0,1,⋯,n−1
所以
⎩⎨⎧aj+1=aj+bjhj+cjhj2+djhj3bj+1=bj+2cjhj+3djhj2cj+1=cj+3djhj,j=0,1,⋯,n−1
把最后一个式子代入前两个式子,消去 dj,得到
{aj+1=aj+bjhj+3hj2(2cj+cj+1)bj+1=bj+hj(cj+cj+1),j=0,1,⋯,n−1
为了减少未知数,我们有
aj+1=aj+bjhj+3hj2(2cj+cj+1)bj+1=bj+hj(cj+cj+1)⇒{bj=hj1(aj+1−aj)−3hj(2cj+cj+1)bj−1=hj−11(aj−aj−1)−3hj−1(2cj−1+cj)⇒bj=bj−1+hj−1(cj−1+cj)
所以
⎩⎨⎧bjbj−1bj=hj1(aj+1−aj)−3hj(2cj+cj+1)=hj−11(aj−aj−1)−3hj−1(2cj−1+cj)=bj−1+hj−1(cj−1+cj)⇒hj1(aj+1−aj)−3hj(2cj+cj+1)=hj−11(aj−aj−1)−3hj−1(2cj−1+cj)+hj−1(cj−1+cj)⇒hj−1cj−1+2(hj−1+hj)cj+hjcj+1=hj3(aj+1−aj)−hj−13(aj−aj−1)(j=1,2,⋯,n−1)
因为 aj, hj 已知,所以上式未知量仅为 cj,而且求出 cj 后,bj 也就求出了。(bj=hj1(aj+1−aj)−3hj(2cj+cj+1))
所以我们有 n−1 个方程,n+1 个未知数,所以我们需要额外的两个方程。
Natural boundary | 自由边界
书上给的是 S′′(a)=S′′(b)=0,实际上,我们在做题中扩展到了 S′′(a)=s0,S′′(b)=sn,此时
c0=2S′′(a)=2s0,cn=2S′′(b)=2sn
所以,我们可以将上面的方程组写成 Ax=b 的形式,其中 A 为 (n+1)×(n+1) 的矩阵
A=1h00⋮0002(h0+h1)h1⋮000h12(h1+h2)⋮00⋯⋯⋯⋱⋯⋯000⋮hn−20000⋮2(hn−2+hn−1)0000⋮hn−11
b 和 x 为 (n+1)×1 的向量
b=2s0h13(a2−a1)−h03(a1−a0)h23(a3−a2)−h13(a2−a1)⋮hn−13(an−an−1)−hn−23(an−1−an−2)2sn,x=c0c1c2⋮cn−1cn
因为矩阵 A 是严格对角占优的,所以该方程组有唯一解。
伪代码

固支边界
固支边界要求 S′(a)=f′(a),S′(b)=f′(b)。
因为 f′(a)=S′(a)=S′(x0)=b0,f′(b)=S′(b)=S′(xn)=bn,所以
⇒{f′(a)f′(b)=b0=h01(a1−a0)−3h0(2c0+c1)=bn=bn−1+hn−1(cn−1+cn)=hn−11(an−an−1)+3hn−1(cn−1+2cn){2h0c0+h0c1hn−1cn−1+2hn−1cn=h03(a1−a0)−3f′(a)=3f′(b)−hn−13(an−an−1)
所以,我们可以将上面的方程组写成 Ax=b 的形式,其中 A 为 (n+1)×(n+1) 的矩阵
A=2h0h00⋮00h02(h0+h1)h1⋮000h12(h1+h2)⋮00⋯⋯⋯⋱⋯⋯000⋮hn−20000⋮2(hn−2+hn−1)hn−1000⋮hn−12hn−1
b 和 x 为 (n+1)×1 的向量
b=h03(a1−a0)−3f′(a)h13(a2−a1)−h03(a1−a0)h23(a3−a2)−h13(a2−a1)⋮hn−13(an−an−1)−hn−23(an−1−an−2)3f′(b)−hn−13(an−an−1),x=c0c1c2⋮cn−1cn
因为矩阵 A 是严格对角占优的,所以该方程组有唯一解。
伪代码

Properties of cubic splines | 三次样条的性质
- 只要系数矩阵严格对角占优(实际上是确保可逆),三次样条就可以由其边界条件唯一确定。
- 如果 minhimaxhi 有界,那么 S(x) 是收敛的。
- 增加点可以更贴近原函数。
Chapter 4 数值微分与积分 | Numerical Differentiation and Integration
4.1 数值微分 | Numerical Differentiation
两点法
最简单的方法:用两个点,取h>0
Forward : f′(x)=hf(x+h)−f(x)+O(h)
Backward : f′(x)=hf(x)−f(x−h)+O(h)
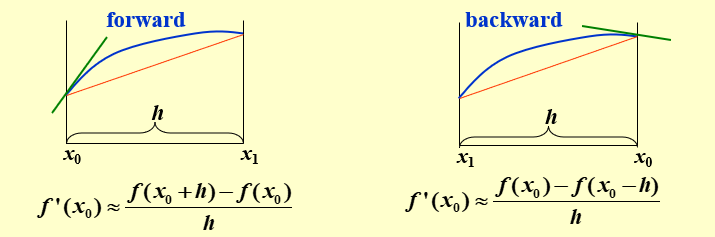
构造由 x0 和 x0+h 确定的一次 Lagrange 插值多项式:
f(x)f′(x)f′(x0)=x0−x0−hf(x0)(x−x0−h)+x0+h−x0f(x0+h)(x−x0)+2!(x−x0)(x−x0−h)f′′(ξx)=hf(x0+h)−f(x0)+22(x−x0)−hf′′(ξx)+2!(x−x0)(x−x0−h)dxdf′′(ξx)=hf(x0+h)−f(x0)−2hf′′(ξx)
一般方法
用 n+1 个点,构造 n 次 Lagrange 插值多项式:
f(x)f′(xj)=k=0∑nf(xk)Lk(x)+(n+1)!(x−x0)⋯(x−xn)f(n+1)(ξx)=k=0∑nf(xk)Lk′(xj)+(n+1)!f(n+1)(ξj)k=0,k=j∏n(xj−xk)
总体而言,更多的评估点会产生更高的准确性。另一方面,功能评估的数量增加,舍入误差也会增加。因此,数值微分是不稳定的!
三点公式
因为
L0(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)
所以
L0′(x)=(x0−x1)(x0−x2)2x−x1−x2
同理有
L1′(x)=(x1−x0)(x1−x2)2x−x0−x2
L2′(x)=(x2−x0)(x2−x1)2x−x0−x1
所以
f′(xj)=f(x0)(x0−x1)(x0−x2)2xj−x1−x2+f(x1)(x1−x0)(x1−x2)2xj−x0−x2+f(x2)(x2−x0)(x2−x1)2xj−x0−x1+3!f(3)(ξj)k=0,k=j∏2(xj−xk)
如果 x0,x1,x2 等距,即 x1=x0+h,x2=x0+2h,则
f′(xj)=f(x0)2h22xj−2x0−3h+f(x1)−h22xj−2x0−2h+f(x2)2h22xj−2x0−h+3!f(3)(ξj)k=0,k=j∏2(xj−xk)
所以
f′(x0)f′(x1)f′(x2)=h1(−23f(x0)+2f(x0+h)−21f(x0+2h))+3h2f(3)(ξ0)=h1(−21f(x0)+21f(x0+2h))−6h2f(3)(ξ1)=h1(21f(x0)−2f(x0+h)+23f(x0+2h))+3h2f(3)(ξ2)
显然,中间的点误差最小,所以,我们可以用这种方法来估计导数值,即
f′(x0)=2h1[f(x0+h)−f(x0−h)]−6h2f(3)(ξ1)
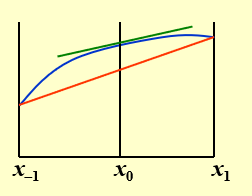
二阶导数
将函数 f 在 x0 处展开为三阶 Taylor 多项式,并求在 x0+h 和 x0−h 处的值:
f(x0+h)=f(x0)+f′(x0)h+21f′′(x0)h2+61f′′′(x0)h3+241f(4)(ξ1)h4f(x0−h)=f(x0)−f′(x0)h+21f′′(x0)h2−61f′′′(x0)h3+241f(4)(ξ−1)h4
将上面两式相加,得
f′′(x0)=h2f(x0+h)−2f(x0)+f(x0−h)−24h2[f(4)(ξ1)+f(4)(ξ−1)]
由于 f(4) 是连续函数,所以存在 ξ 使得
f(4)(ξ)=21[f(4)(ξ1)+f(4)(ξ−1)]
所以
f′′(x0)=h2f(x0+h)−2f(x0)+f(x0−h)−12h2f(4)(ξ)
4.3 数值积分基础 | Elements of Numerical Integration
对于没有显式原函数或原函数难以计算的函数,我们通过 数值求积(Numerical Quadrature) 来近似计算积分值:使用和 i=0∑naif(xi) 来近似计算积分值 ∫abf(x)dx。
为了确定系数 ai ,我们给出一种求积方法:
以第三章中给出的插值多项式为基础,得到 Lagrange 插值多项式:
Pn(x)=i=0∑nf(xi)Li(x)
所以
∫abf(x)dx≈∫abPn(x)dx=i=0∑nf(xi)∫abLi(x)dx=i=0∑nf(xi)ai
误差项为
∫abf(x)dx−i=0∑nf(xi)ai=∫ab(f(x)−Pn(x))dx=∫ab(n+1)!f(n+1)(ξ)i=0∏n(x−xi)dx
精确度 | Precision
求积公式的精确度 (precision/degree of accuracy) 是使得求积公式对 xk 精确成立的最大正整数 k。
通用法则 - Newton-Cotes 求积公式
在等距节点上(h=nb−a),考察系数 ai 的值,我们可以得到一些通用的求积法则:
ai=∫x0xnLi(x)dx=∫x0xnj=0,j=i∏nxi−xjx−xjdx
令 x=a+th,则
ai=∫x0xnj=0,j=i∏nxi−xjx−xjdx=∫0nj=0,j=i∏n(i−j)h(t−j)h⋅hdt=h⋅i!(n−i)!(−1)n−i⋅∫0nj=0,j=i∏n(t−j)dt
梯形法则 | Trapezoidal Rule
当 n=1 时:
aia0a1=h⋅i!(1−i)!(−1)1−i⋅∫01j=0,j=i∏1(t−j)dt=h⋅0!(1−0)!(−1)1−0⋅∫01(t−1)dt=21h=h⋅1!(1−1)!(−1)1−1⋅∫01(t−0)dt=21h
此时,n=1 的求积公式为
∫abf(x)dx=2h[f(a)+f(b)]−12h3f′′(ξ)
此即为 梯形法则(Trapezoidal Rule)。
精确度
梯形法则的精确度为 k=1。
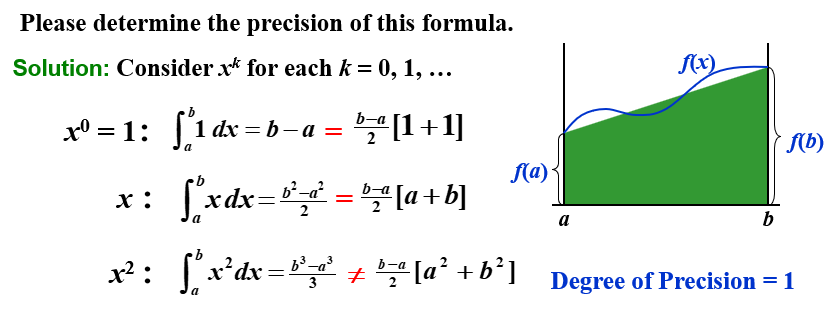
Simpson 法则 | Simpson's Rule
当 n=2 时:
aia0a1a2=h⋅i!(2−i)!(−1)2−i⋅∫02j=0,j=i∏2(t−j)dt=h⋅0!(2−0)!(−1)2−0⋅∫02(t−1)(t−2)dt=31h=h⋅1!(2−1)!(−1)2−1⋅∫02(t−0)(t−2)dt=34h=h⋅2!(2−2)!(−1)2−2⋅∫02(t−0)(t−1)dt=31h
此时,n=2 的求积公式为
∫abf(x)dx=3h[f(a)+4f(2a+b)+f(b)]−90h5f(4)(ξ)
此即为 Simpson 法则(Simpson's Rule)。
其精确度为 k=3。
Simpson 3/8 法则 | Simpson's 3/8 Rule
当 n=3 时,求积公式为
∫abf(x)dx=83h[f(a)+3f(32a+b)+3f(3a+2b)+f(b)]−803h5f(4)(ξ)
其精确度为 k=3。
Cotes 求积公式 | Cotes Rule
当 n=4 时,求积公式为
∫abf(x)dx=452h[7f(a)+32f(43a+b)+12f(2a+b)+32f(4a+3b)+7f(b)]−9458h7f(6)(ξ)
通用法则的一般结论
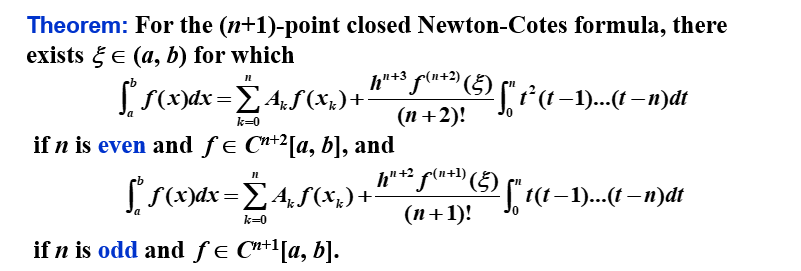
注意:当 n 是偶数时,精度的次数为 n+1,即使插值多项式的次数至多为 n。在 n 是奇数的情况,精度的次数仅为 n。
4.4 复合数值积分 | Composite Numerical Integration
Newton-Cotes 以等距节点的插值多项式为基础。由于高次多项式的振荡性,这个过程在大的区间上是不精确的。为了解决这个问题,我们采用低阶 Newton-Cotes 的分段(piecewise)方法。
复合梯形法则 | Composite Trapezoidal Rule
将区间 [a,b] 分成 n 个子区间,每个子区间长度为 h=nb−a,则
∫xk−1xkf(x)dx≈2xk−xk−1[f(xk−1)+f(xk)], k=1,...,n
∫abf(x)dx=i=0∑n−1∫xixi+1f(x)dx=2h[f(a)+2j=1∑n−1f(xj)+f(b)]=Tn
其中,xi=a+ih,ξ∈[a,b]。
误差项为
∫abf(x)dx−Tn=12h2(b−a)f′′(ξ)
复合 Simpson 法则 | Composite Simpson's Rule
将区间 [a,b] 分成 n 个子区间,每个子区间长度为 h=nb−a,则
∫xkxk+1f(x)dx≈6h[f(xk)+4f(xk+21)+f(xk+1)]
∫abf(x)dx≈6h[f(a)+4k=0∑n−1f(xk+21)+2k=0∑n−2f(xk+1)+f(b)]=Sn
其中,xi=a+ih,ξ∈[a,b]。
误差项为
∫abf(x)dx−Sn=−180b−a(2h)4f(4)(ξ)
为简化表达,我们取 n′=2n,则 h′=n′b−a=2h,x2k=xk,x2k+1=xk+2h,则
∫abf(x)dx≈3h′[f(a)+4oddk∑f(xk)+2evenk∑f(xk)+f(b)]=Sn′
例题

舍入误差的稳定性
所有的复合积分方法共有的一个重要性质是 舍入误差的稳定性。
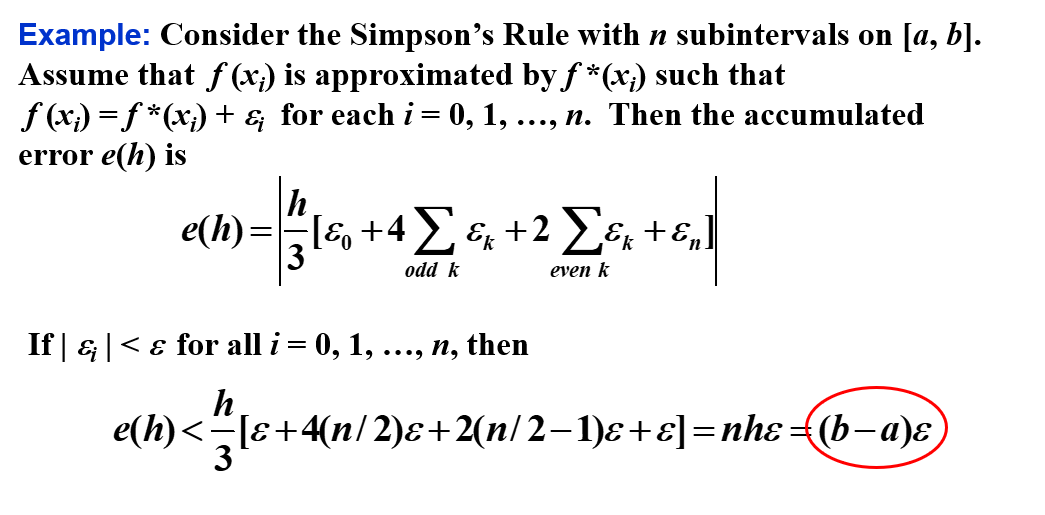
可见,误差界与 h 和 n 无关。这说明即使将一个区间分成更多子区间,也不会增加舍入误差。
4.5 Romberg 积分 | Romberg Integration
考察残差项,对于梯形法则,有
R2n[f]=−(2h)2121(b−a)f′′(ξ)≈41Rn[f]
所以
I−TnI−T2n≈41
即
I≈4−14T2n−Tn=34T2n−31Tn=Sn
同理,总体上,我们有
4−14T2n−Tn=Sn,42−142S2n−Sn=Cn,43−143C2n−Cn=Rn,...
这里的 Rn 就是 Romberg 积分。
所以算法为:
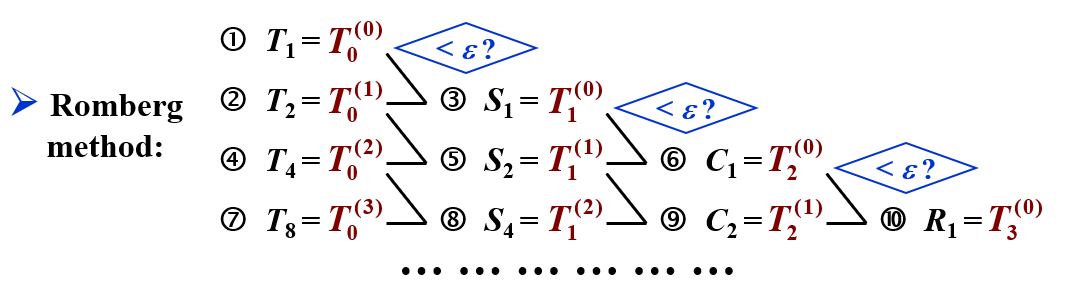
其中,每一步计算误差有没有到,如果没到,继续向后算。
伪代码

Target:使用低阶公式产生高精度的结果。

4.6 自适应求积方法 | Adaptive Quadrature Methods
Target: 预测函数变化的大小,使步长适应变化的需求。
其实就是先整体估摸着求积,然后看看精度如何(此处判断精度的方式是与上一次得到的值作比较,以比值为判断条件——如果本次和上次的值差不多,说明趋于收敛);如果不够,就再细分一下,再求积。
举个例子:
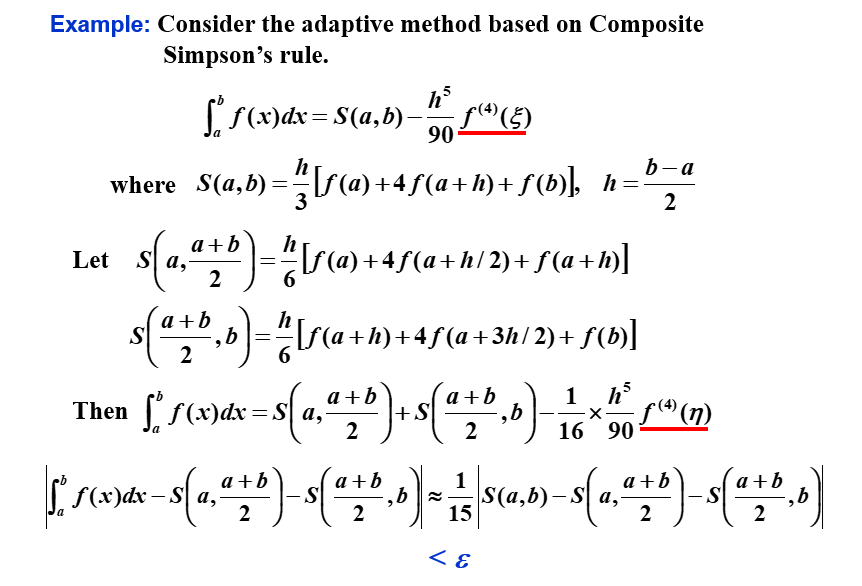
这里可以看到,S(a,2a+b)+S(2a+b,b) 逼近 ∫abf(x)dx 的效果比 S(a,2a+b)+S(2a+b,b) 逼近S(a,b) 好15倍。
4.7 Gauss 求积 | Gauss Quadrature
Target: 通过选择 n+1 个合适的节点,使得求积公式的精度达到 2n+1。
"例子"
用 Gauss 求积公式,在 n=1 的情况下估计 ∫−11xf(x)dx,则精度为3,需满足 f(x)=1,x,x2,x3。
设 ∫−11xf(x)dx≈A0f(x0)+A1f(x1),则
⎩⎨⎧∫−11xdx=A0+A1∫−11xxdx=A0x0+A1x1∫−11xx2dx=A0x02+A1x12∫−11xx3dx=A0x03+A1x13
由此可求得四个未知数,从而得到求积公式
但是,求解非线性方程组是很困难的,所以我们采用另一种方法。
我们可以证明: x0...xn are Gaussian points iff W(x)=k=0∏n(x−xk) is orthogonal to all the polynomials of degree no greater than n.

所以我们就是要找到一个正交多项式,它的零点就是我们要找的节点。
回到上面那个例子,我们就是要找到一个二阶多项式,其与小于二次的多项式的内积为0。


Gauss-Legendre 求积公式
Legendre 多项式:Pn(x)=2nn!1dxndn[(x2−1)n]。
其内积关系为:(Pk,Pl)={0,2k+12,k=lk=l。
根据 P0(x)=1,P1(x)=x,我们有递推关系:
Pn+1(x)=n+12n+1xPn(x)−n+1nPn−1(x)
这些就是Legendre多项式的集合,也就是我们要找的正交多项式。
Gauss-Chebyshev 求积公式

Chapter 5 常微分方程的初值问题 | Initial-Value Problems for Ordinary Differential Equations
用数值方法来求解常微分方程的初值问题,就是找到 w0,w1,⋯,wN,使得 wi≈y(ti)。
5.1 初值问题的基本理论 | The Elementary Theory of Initial-Value Problems
Lipschitz 条件 | Lipschitz Condition
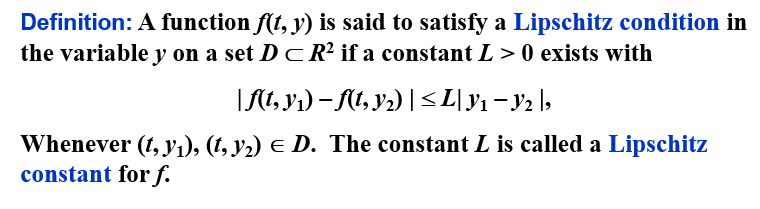
实际上,就是关于 y 的偏导数(如果可导)的上界
在 Lipschitz 条件下,初值问题的解是唯一的:
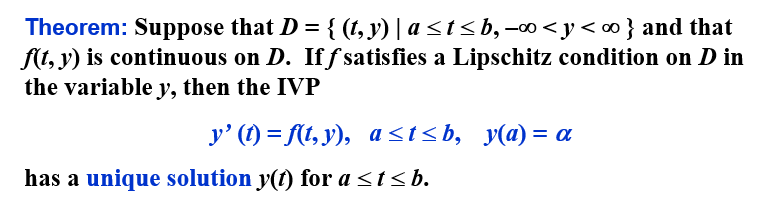
良态问题 | Well-Posed Problems

z(t) 那行的式子是原式的摄动问题(perturbed problem),即在原式的基础上加上一个扰动项(假定微分方程可能有误差δ,或者初值有误差ϵ)
在 Lipschitz 条件下,初值问题是良态的:
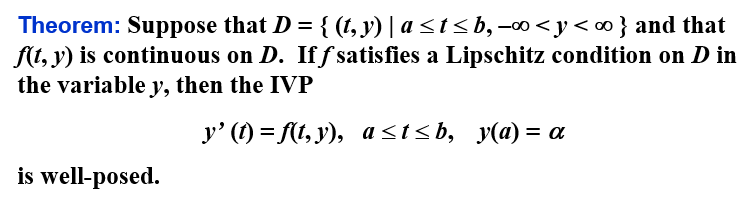
5.2 Euler 法 | Euler's Method
Euler 法的目的是获得如下形式的近似解:
{dtdy=f(t,y)t∈[a,b]y(a)=α
得到的是一系列点的近似值。
Euler 法的思想是,用 f(t,y) 在 (ti,yi) 处的线性近似值来代替 f(t,y),即:
wi+1=wi+hf(ti,wi)
我们称其为差分方程(difference equation)
误差界
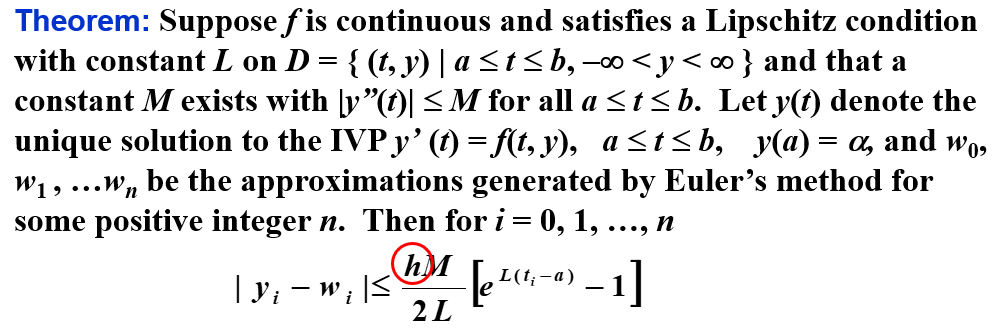
如果考虑每次计算中的舍入误差,则有

此时,往往有 h>2δ/M(δ 通常很小),所以随着 h 的减小,误差会越来越小。(打勾函数的右沿)
其他 Euler 法
隐式欧拉法 | Implicit Euler Method
隐式欧拉法(implicit Euler method),又称后退欧拉法,是按照隐式公式进行数值求解的方法。隐式公式不能直接求解,一般需要用欧拉显式公式得到初值,然后用欧拉隐式公式进行迭代求解。因此,隐式公式比显式公式计算复杂,但稳定性好。

梯形法 | Trapezoidal Method
梯形法(trapezoidal method)是一种求解常微分方程初值问题的数值方法。它是欧拉法和隐式欧拉法的结合,是一种二阶方法。梯形法的基本思想是用 f(ti,yi) 和 f(ti+1,yi+1) 的平均值来代替 f(t,y),即:
wi+1=wi+2h(f(ti,wi)+f(ti+1,wi+1))
Note: The local truncation error is indeed O(h2). However an implicit equation has to be solved iteratively.
双步法 | Double-step Method
双步法相较于之前的方法,需要两个初始值,即 w0 和 w1,然后用这两个初始值来计算 w2,再用 w1 和 w2 来计算 w3,以此类推。

对比
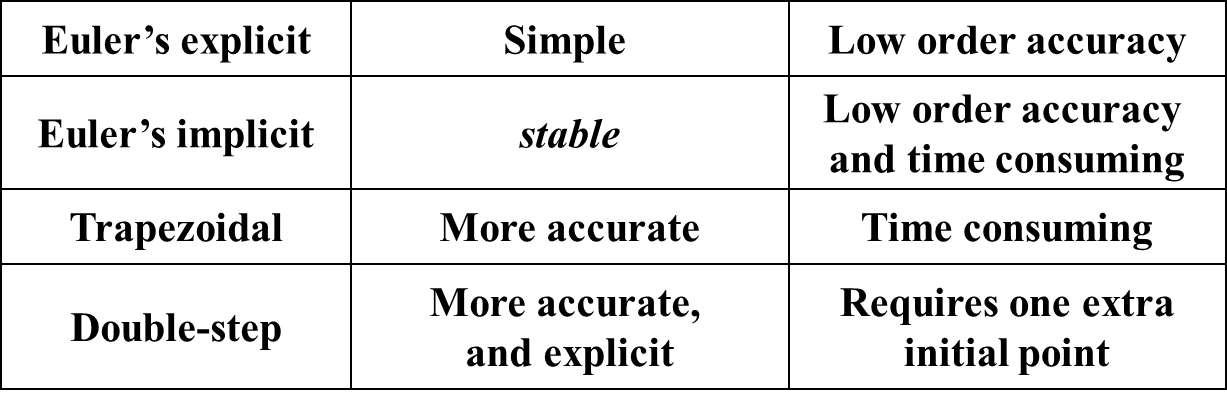
5.3 高阶 Taylor 法 | Higher-Order Taylor Methods
局部截断误差
局部截断误差只考虑一步的误差,即假设前面没有误差:
w0=α
wi+1=wi+hϕ(ti,wi),i=0,1,⋯,N−1
有局部截断误差
τi+1(h)=hyi+1−(yi+hϕ(ti,yi))=hyi+1−yi−ϕ(ti,yi)
"对于 Euler 法"

Euler 法实际上就是高阶 Taylor 法的一阶近似。
高阶 Taylor 法
yi+1=yi+hf(ti,yi)+2h2f′(ti,yi)+⋯+n!hnf(n−1)(ti,yi)+(n+1)!hn+1f(n)(ξi,y(ξi))
n 阶的 Taylor 法:
w0wi+1=α=wi+hT(n)(ti,wi)(i=0,...,n−1)whereT(n)(ti,wi)=f(ti,wi)+2hf′(ti,wi)+...+n!hn−1f(n−1)(ti,wi)
其局部截断误差为 O(hn)(如果 y∈Cn+1[a,b])。
"例子"

求 f(t,y(t))=t2y(t)+t2et 关于 t 的一阶导数
f(t,y(t))f′(t,y(t))=t2y+t2et=t2y′−t22y+2tet+t2et=t2(t2y+t2et)−t22y+2tet+t2et=t24y+2tet−t22y+2tet+t2et=t22y+4tet+t2et
T(2)(ti,wi)=f(ti,wi)+2hf′(ti,wi)=ti2wi+ti2eti+2h(ti22wi+4tieti+ti2eti)
所以 wi+1 的表达式为:
wi+1=wi+hf(ti,wi)+2h2f′(ti,wi)=wi+h(ti2wi+ti2eti)+2h2(ti22wi+4tieti+ti2eti)
h=0.1 时:
| i |
ti |
wi |
y(ti) |
| 0 |
1.00 |
0.0000000 |
0.0000000 |
| 1 |
1.10 |
0.3397852 |
0.3459199 |
| 2 |
1.20 |
0.8521434 |
0.8666425 |
| 3 |
1.30 |
1.581770 |
1.607215 |
| 4 |
1.40 |
2.580997 |
2.620360 |
| 5 |
1.50 |
3.910985 |
3.967666 |
| 6 |
1.60 |
5.643081 |
5.720962 |
| 7 |
1.70 |
7.860382 |
7.963874 |
| 8 |
1.80 |
10.65951 |
10.79362 |
| 9 |
1.90 |
14.15268 |
14.32308 |
| 10 |
2.00 |
18.46999 |
18.68310 |
应用线性插值法,我们有
y(1.04)y(1.55)y(1.97)≈0.6y(1.00)+0.4y(1.10)=0.6∗0.0000000+0.4∗0.3397852=0.1359141≈0.5y(1.50)+0.5y(1.60)=0.5∗3.910985+0.5∗5.643081=4.777033≈0.3y(1.90)+0.7y(2.00)=0.3∗14.15268+0.7∗18.46999=17.17480
其精确值为:
y(1.04)y(1.55)y(1.97)=0.1199875=4.788635=17.27930
5.4 Runge-Kutta 法 | Runge-Kutta Methods
泰勒方法需要计算 f(t,y) 的导数并求值,这是一个复杂、耗时的过程。Runge-Kutta 方法具有 Taylor 方法的高阶局部截断误差,但是不需要计算 f(t,y) 的导数。
二阶 Runge-Kutta 法 | Runge-Kutta method of order 2
我们考察改进欧拉法 K 前面的系数以及 K2 的步长,使局部截断误差为 O(h2):
⎩⎨⎧wi+1K1K2===wi+h[λ1K1+λ2K2]f(ti,wi)f(ti+ph,wi+phK1)

这有无穷多种可能,我们称其为 二阶 Runge-Kutta 方法(Runge-Kutta method of order 2)。
以下三个是二阶 Runge-Kutta 方法的特例
中点法 | Midpoint Method
{w0=αwi+1=wi+hf(ti+2h,wi+2hf(ti,wi))
改进欧拉法 | Modified Euler Method
⎩⎨⎧w0=αwi+1=wi+h(21K1+21K2)K1=f(ti,wi)K2=f(ti+h,wi+hK1)
"是不是感觉和梯形法很像?"
梯形法是用 f(ti,wi) 和 f(ti+1,wi+1) 的平均值来代替 f(t,y),而改进欧拉法是用 f(ti,wi) 和 f(ti+h,wi+hK1) 的平均值来代替 f(t,y)。区别在于前者是隐式的,后者是显式的。
Heun 法 | Heun's Method
⎩⎨⎧w0=αwi+1=wi+h(41K1+43K2)K1=f(ti,wi)K2=f(ti+32h,wi+32hK1)
高阶 Runge-Kutta 法 | Runge-Kutta methods of order m
⎩⎨⎧w0=αwi+1=wi+h(λ1K1+λ2K2+⋯+λmKm)K1=f(ti,wi)K2=f(ti+α2h,wi+β21hK1)K3=f(ti+α3h,wi+β31hK1+β32hK2)⋮Km=f(ti+αmh,wi+βm1hK1+βm2hK2+⋯+βm,m−1hKm−1)
"Order 4-the most popular one"
⎩⎨⎧w0=αwi+1=wi+h(61K1+31K2+31K3+61K4)K1=f(ti,wi)K2=f(ti+2h,wi+2hK1)K3=f(ti+2h,wi+2hK2)K4=f(ti+h,wi+hK3)
我们给出每步的求值次数和局部阶段误差的阶之间的关系:
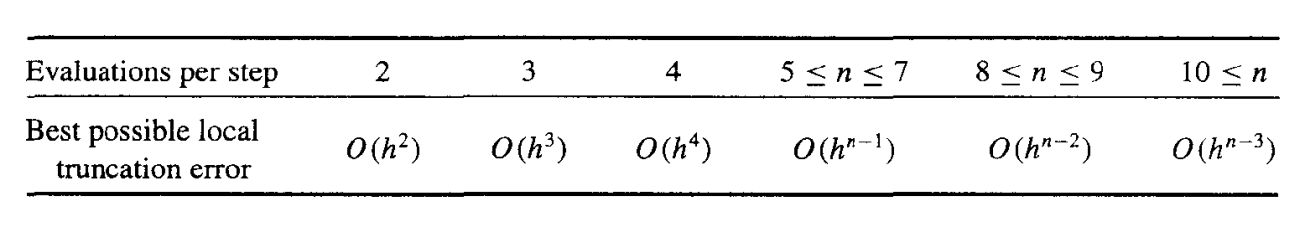
这说明了为什么人们更喜欢使用具有较小步长的小于 5 阶的 Runge-Kutta 方法。
因为 Runge-Kutta 方法是基于 Taylor 展开的,所以 y 必须足够平滑,才能获得更高阶方法的更高精度。通常情况下,人们更喜欢使用较小步长的低阶方法,而不是使用较大步长的高阶方法。
如果 y 不够光滑,那么高阶的 Runge-Kutta 方法也不会有很好的效果,所以一般会用低阶的 Runge-Kutta 方法,但是步长会更小
5.6 多步法 | Multistep Methods
在一些网格点(mesh points)上使用 y 和 y′ 的线性组合来更好地近似 y(ti+1)
求解初值问题
y′=f(t,y),a≤t≤b,y(a)=α
的 m 步多步法(m-step multistep method)的一般形式为
wi+1=+am−1wi+am−2wi−1+...+a0wi+1−mh[bmf(ti+1,wi+1)+bm−1f(ti,wi)+...+b0f(ti+1−m,wi+1−m)]
其中 h=(b−a)/N,给定 m 个初始值 w0,w1,...,wm−1,a0,a1,...,am−1 和 b0,b1,...,bm 是常数。
bm=0 的方法称为显式(explicit);bm=0 的方法称为隐式(implicit)
局部截断误差(local truncation error)为
τi+1(h)=hyi+1−wi+1=hyi+1−am−1yi−am−2yi−1−...−a0yi+1−m−bmf(ti+1,yi+1)−bm−1f(ti,yi)−...−b0f(ti+1−m,yi+1−m)
Adams-Bashforth 显式 m 步方法 | Adams-Bashforth explicit m-step technique
注意到
y(ti+1)=y(ti)+∫titi+1f(t,y(t))dt
为了推导 Adams-Bashforth 显式 m 步方法,我们通过(ti,f(ti,y(ti))),(ti−1,f(ti−1,y(ti−1))),(ti−2,f(ti−2,y(ti−2))),...,(ti+1−m,f(ti+1−m,y(ti+1−m))) 形成向后差分多项式 Pm−1(t),然后用 Pm−1(t) 来代替 f(t,y(t)),从而得到
f(t,y(t))=Pm−1(t)+m!f(m)(ξi,y(ξi))(t−ti)(t−ti−1)...(t−ti+1−m)
"向后差分多项式"
Pn(xs)=k=0∑n(−1)k(−sk)∇kf(xn)
∫titi+1f(t,y(t))dt=∫titi+1Pm−1(t)dt+∫titi+1Rm−1(t)dt=h∫01Pm−1(ti+sh)ds+h∫01Rm−1(ti+sh)ds=hk=0∑m−1∇kf(ti,y(ti))(−1)k∫01(−sk)ds+m!hm+1∫01f(m)(ξi,y(ξi))s(s+1)...(s+m−1)ds
其中 Rm−1(t) 是余项,也就是截断误差。
我们有
wi+1∫titi+1Rm−1(t)dt=wi+h∫01Pm−1(ti+sh)ds=wi+hk=0∑m−1∇kf(ti,y(ti))(−1)k∫01(−sk)ds=m!hm+1∫01f(m)(ξi,y(ξi))s(s+1)...(s+m−1)ds=m!hm+1f(m)(μi,y(μi))∫01s(s+1)...(s+m−1)ds=hm+1f(m)(μi,y(μi))(−1)m∫01(−sm)ds
其局部截断误差为
τi+1(h)=hyi+1−am−1yi−am−2yi−1−...−a0yi+1−m−bmf(ti+1,yi+1)−bm−1f(ti,yi)−...−b0f(ti+1−m,yi+1−m)=h1∫titi+1Rm−1(t)dt=hmf(m)(μi,y(μi))(−1)m∫01(−sm)ds
"(−1)k∫01(−sk)ds"
| k |
(−1)k∫01(−sk)ds |
| 0 |
1 |
| 1 |
21 |
| 2 |
125 |
| 3 |
83 |
| 4 |
720251 |
| 5 |
28895 |
"2步"
取 m=2,我们有
wi+1=wi+h[∇0f(ti,wi)+21∇1f(ti,wi)]=wi+h[23f(ti,wi)−21f(ti−1,wi−1)]
因为 yi+1=yi+h[bmf(ti+1,wi+1)+bm−1f(ti,wi)+...+b0f(ti+1−m,wi+1−m)]+∫titi+1Rm−1(t)dt,所以
其局部截断误差为
τi+1(h)=hmf(m)(μi,y(μi))(−1)m∫01(−sm)ds=125h2f′′(μi,y(μi))=125h2y′′′(μi)
| m |
fi |
fi−1 |
fi−2 |
fi−3 |
| 1 |
1 |
− |
− |
− |
| 2 |
23 |
−21 |
− |
− |
| 3 |
1223 |
−34 |
125 |
− |
| 4 |
2455 |
−2459 |
2437 |
−83 |
查表可得,Adams-Bashforth 显式 4 步方法的为
wi+1=wi+24h(55fi−59fi−1+37fi−2−9fi−3)
Adams-Moulton 隐式 m 步方法 | Adams-Moulton implicit m-step technique
同样的,我们采用向前差分多项式,可以得到 Adams-Moulton 隐式 m 步方法:

Adams 预测-校正系统 | Adams predictor-corrector system
Adams 预测-校正系统是 Adams-Bashforth 显式 m 步方法和 Adams-Moulton 隐式 m 步方法的结合:
- 用 Runge-Kutta 法计算出 m 个初始值 w0,w1,...,wm−1 (如果初值的个数不够)
- 预测:用 Adams-Bashforth 显式 m 步方法计算出 wm,wm+1,... 直到 wN−1
- 校正:用 Adams-Moulton 隐式 m 步方法计算出 wm,wm+1,... 直到 wN−1
在这三步中使用的所有公式的局部截断误差的阶必须相同。
最常用的系统是以 4 阶 Adams-Bashforth 方法作为预测器,以 Adams-Moulton 方法的一次迭代作为校正器,其起始值来自 4 阶 Runge-Kutta 方法。
宏观角度:Taylor 展开

通过对比系数,可以有一族解。
通过对这个解的再限制(添加两个条件),我们可以得到多种方法。

5.9 高阶方程和微分方程组 | Higher-Order Equations and Systems of Differential Equations
微分方程组的矩阵形式
对 m 阶微分方程组:
⎩⎨⎧u1′(t)=f1(t,u1(t),u2(t),...,um(t))⋮um′(t)=fm(t,u1(t),u2(t),...,um(t))
给定 m 个初始值 u1(a),u2(a),...,um(a),我们可以用 m 步的 Runge-Kutta 法来求解。
用矩阵的形式可以记作
{y′(t)=f(t,y(t))y(a)=α
高阶微分方程的转化

"例题"

"modified Euler's method"
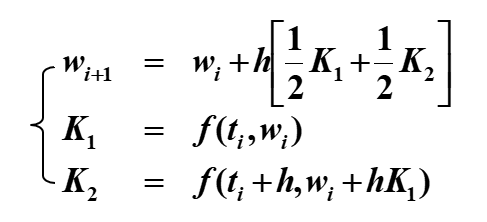
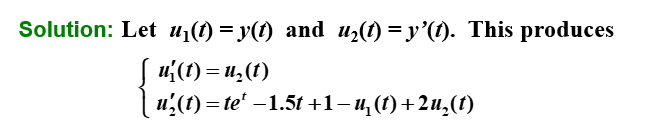
"第一次迭代:"

"第二次迭代:"
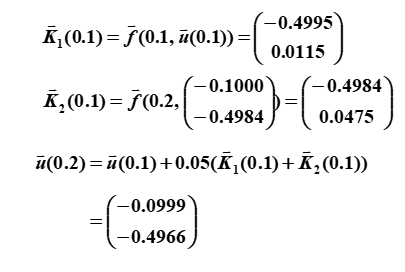
5.10 稳定性 | Stability
相容 | Consistency
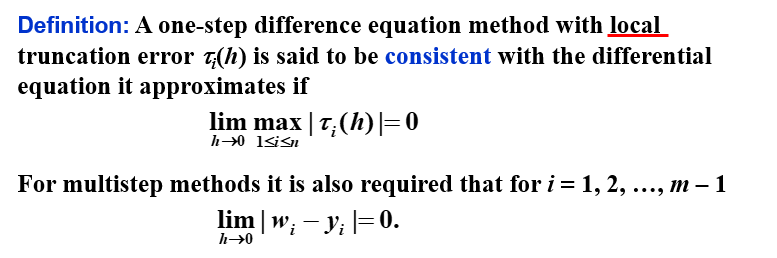
收敛 | Convergence
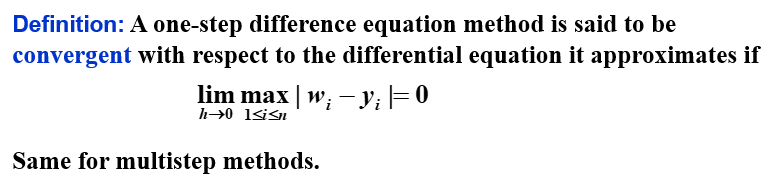
稳定性 | Stability
除了这两个概念,我们还需要一个概念:稳定性。如果初始条件的小变化或扰动会导致后续近似值的相应小变化,则该方法被称为稳定。
特征方程与稳定性
已知方程
w0wi+1=α,w1=α1,⋯,wm−1=αm−1=am−1wi+am−2wi−1+⋯+a0wi+1−m+hF(ti,h,wi+1,wi,⋯,wi+1−m)
我们给出一个相关的多项式,称为特征多项式(characteristic polynomial):
P(λ)=λm−am−1λm−1−am−2λm−2−⋯−a0
- 如果 P(λ) 的所有根的模都小于等于 1,且取等时为单根,则称该方法满足根条件(root condition)
- 如果有且仅有一个根的模等于 1,则该方法是强稳定(strongly stable)的
- 如果有多个根的模等于 1,则该方法是弱稳定(weakly stable)的
- 如果方法不满足根条件,则该方法是不稳定的
测试方程 | Test Equation
我们将一个特定的方法应用于一个简单的测试方程:
y’=λy,y(0)=α,where Re(λ)<0
假设舍入误差只在初始点引入。如果这个初始误差会在某个步长 h 下减小,那么这个方法就被称为绝对稳定(absolutely stable),此时 H=λh。所有这样的 H 的集合构成了绝对稳定域(region of absolute stability)。
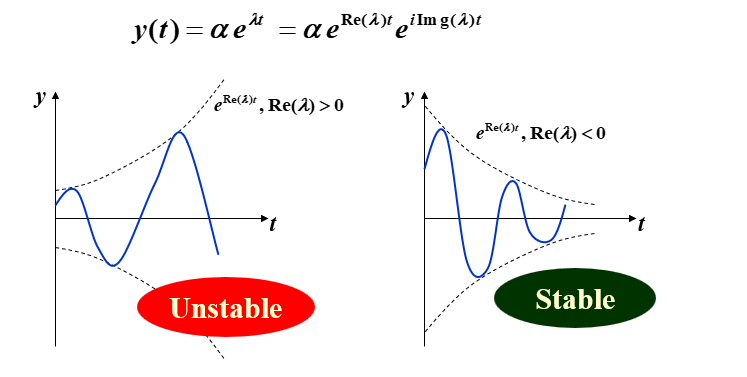
如果方法 A 的绝对稳定域比方法 B 的大,那么方法 A 就比方法 B 更稳定
显式 Euler 法的稳定性
在显式 Euler 法中,我们有
wi+1=wi+hf(ti,wi)
在这个测试方程中,我们有
wi+1=(1+λh)wi=(1+H)wi=(1+H)i+1α
我们给初值加上一个扰动项 ϵ,即 α∗=α+ϵ,则
wi+1∗=(1+H)i+1(α+ϵ)
所以
ϵi+1=(1+H)i+1ϵ
要确保稳定性,我们需要 ∣(1+H)i+1∣<1,即 ∣1+H∣<1。
隐式 Euler 法的稳定性
在隐式 Euler 法中,我们有
wi+1=wi+hf(ti+1,wi+1)
在这个测试方程中,我们有
wi+1=wi+hλwi+1
所以
wi+1=1−hλ1wi=1−H1wi=(1−H1)i+1α
我们给初值加上一个扰动项 ϵ,即 α∗=α+ϵ,则
wi+1∗=(1−H1)i+1(α+ϵ)
所以
ϵi+1=(1−H1)i+1ϵ
要确保稳定性,我们需要 ∣(1−H1)i+1∣<1,即 ∣1−H1∣<1。
二阶 隐式 Runge-Kutta 法的稳定性
在二阶 隐式 Runge-Kutta 法中,我们有
{wi+1K1==wi+hK1f(ti+21h,wi+21hK1)
在这个测试方程中,我们有
K1wi+1=λ(wi+21hK1)⇒K1=1−21hλλwi=wi+hK1=wi+h1−21hλλwi=wi+1−21HHwi=2−H2+Hwi=(2−H2+H)i+1α
我们给初值加上一个扰动项 ϵ,即 α∗=α+ϵ,则
wi+1∗=(2−H2+H)i+1(α+ϵ)
所以
ϵi+1=(2−H2+H)i+1ϵ
要确保稳定性,我们需要 ∣2−H2+H∣<1。
四阶 显式 Runge-Kutta 法的稳定性
在四阶 显式 Runge-Kutta 法中,我们有
⎩⎨⎧wi+1K1K2K3K4=====wi+6h(K1+2K2+2K3+K4)f(ti,wi)f(ti+21h,wi+21hK1)f(ti+21h,wi+21hK2)f(ti+h,wi+hK3)
在这个测试方程中,我们有
K1K2K3K4wi+1=λwi=λ(wi+21hK1)=λwi(1+21H)=λ(wi+21hK2)=λwi(1+21H+41H2)=λ(wi+hK3)=λwi(1+H+21H2+41H3)=wi+6h(K1+2K2+2K3+K4)=wi+6hλwi(1+2(1+21H)+2(1+21H+41H2)+(1+H+21H2+41H3))=wi+6Hwi(6+3H+H2+41H3)=wi(1+H+21H2+61H3+241H4)=α(1+H+21H2+61H3+241H4)i+1
我们给初值加上一个扰动项 ϵ,即 α∗=α+ϵ,则
wi+1∗=α∗(1+H+21H2+61H3+241H4)i+1
所以
ϵi+1=(1+H+21H2+61H3+241H4)i+1ϵ
要确保稳定性,我们需要 ∣1+H+21H2+61H3+241H4∣<1。
微分方程组
考虑一个微分方程组
⎩⎨⎧u1′u2′=9u1+24u2+5cost−31sint,=−24u1−51u2−9cost+31sint,u1(0)u2(0)=34=32
应用欧拉显式法,我们该如何选择步长 h 才能保证稳定性?
我们将条件改写为矩阵形式:
(u1′u2′)=(9−2424−51)(u1u2)+(5cost−31sint−9cost+31sint)
应用欧拉显式法,我们有
(u1i+1u2i+1)=(u1iu2i)+h(9−2424−51)(u1iu2i)+h(5costi−31sinti−9costi+31sinti)
记 A=(9−2424−51),则
(u1i+1u2i+1)=(I+hA)(u1iu2i)+h(5costi−31sinti−9costi+31sinti)
我们给初值加上一个扰动项 ϵ0 和 μ0,即 u0∗=u0+(ϵ0μ0),则
(u1i+1∗u2i+1∗)=(I+hA)(u1i∗u2i∗)+h(5costi−31sinti−9costi+31sinti)
上面两个式子相减,我们有
(ϵi+1μi+1)=(I+hA)(ϵiμi)
所以
(ϵi+1μi+1)=(I+hA)i+1(ϵ0μ0)
要确保稳定性,我们需要 ∣(I+hA)i+1∣<1。
也就是说,我们需要 ∣1+hλ∣<1⇔−2<hλ<0,其中 λ 是 A 的特征值。
我们求解 A 的特征值,得到 λ1=−3 和 λ2=−39。
所以,我们需要 −2<hλ1<0⇔32>h>0 和 −2<hλ2<0⇔392>h>0。
所以,我们需要 0<h<392。
Chapter 6 解线性方程组的直接法 | Direct Methods for Solving Linear Systems
6.1 回代的Gauss消去法 | Gaussian elimination with backward substitution
算法内容
解方程组Ax=b,记A(1)=A=aij(1),b(1)=b=b1(1)b2(1)⋮bn(1),x(1)=x=x1(1)x2(1)⋮xn(1),则增广矩阵A~为:
A~=a11(1)a21(1)⋮an1(1)a12(1)a22(1)⋮an2(1)⋯⋯⋱⋯a1n(1)a2n(1)⋮ann(1)b1(1)b2(1)⋮bn(1)
通过高斯消元我们可以得到新的增广矩阵A~(k):
A~(k)=a11(k)0⋮0a12(k)a22(k)⋮0⋯⋯⋱⋯a1n(k)a2n(k)⋮ann(k)b1(k)b2(k)⋮bn(k)
第1次迭代过程为:如果 a11(1)=0 ,记 mi1=ai1(1)/a11(1) ,则
{aij(2)=aij(1)−mi1a1j(1)bi(2)=bi(1)−mi1b1(1)
第t次迭代过程为:如果att(t)=0,记 mit=ait(t)/att(t) ,则
{aij(t+1)=aij(t)−mitatj(t)bi(t+1)=bi(t)−mitbt(t)
如果att(t)=0,则交换第t行与第k行,使得akk(k)=0,然后再进行第k次迭代。如果找不到akk(k)=0,则方程组没有唯一解,算法停止。
写成伪代码如下:

计算次数
由于在计算机上完成乘法或除法所需的时间大致相同,且大于完成加法或减法所需的时间,所以我们分开考虑乘法和除法的计算次数。
对上述算法进行分析,可以得到计算次数如下:
消元过程
在每个 i 中,
Step 5 需要完成 n−i 次除法,Step 6 由 Ej−mjiEi 代替方程 Ej 的过程中,对每个 j ,需要完成 n−i+1 次乘法和 n−i+1 次减法。所以共需要完成 (n−i)(n−i+1) 次乘法和 (n−i)(n−i+1) 次减法。
所以,消元过程共需要完成 i=1∑n−1((n−i)+(n−i)(n−i+1)) 次乘法/除法和 i=1∑n−1(n−i)(n−i+1) 次加法/减法。
即消元过程共需要完成 31n3+21n2−65n 次乘法/除法和 31n3−31n 次加法/减法。
回代过程
Step 8 需要完成 1 次除法。
在每个 i 中,
Step 9 需要完成 n−i 次乘法和 n−i−1 次加法(对每个相加项),然后是一次减法和一次除法。
所以,回代过程共需要完成 1+i=1∑n−1((n−i)+1) 次乘法/除法和 i=1∑n−1(n−i) 次加法/减法。
即回代过程共需要完成 21n2+21n 次乘法/除法和 21n2−21n 次加法/减法。
总计算次数
乘法/除法:
(31n3+21n2−65n)+(21n2+21n)=31n3+n2−31n
加法/减法:
(31n3−31n)+(21n2−21n)=31n3+21n2−65n
从这里我们可以得知,高斯消元法的算法复杂度为O(N3)
6.2 选主元策略 | Pivoting Strategies
在上个算法中,我们观察到,如果与ajk(k)相比,∣akk(k)∣很小,那么乘数mik(k)=akk(k)aik(k)就会很大,这样就会导致误差的积累。而且在代换时,xk(k)的值也会很大,这样就会导致误差的积累。所以我们需要选取一个合适的主元,使得误差的积累最小。
部分主元选取策略 | Partial Pivoting
我们考虑选择一个比较大的元素作为主元,这样就可以减小误差的积累。
所以我们可以在每次迭代时,从第k行开始,选取该列中绝对值最大的元素作为主元,然后再进行消元。
"伪代码如下:"


比例因子选取策略 | Scaling Partial Pivoting
这个方法通过比较"每一行的元素都除以该行的最大元素的绝对值",然后通过这个结果进行部分主元选取策略,再对原方程组部分进行行交换,从而选取主元。
这里的比例因子就是每一行的最大元素的绝对值,即
si=1≤j≤nmax∣aij∣
比例因子只在初始过程中计算一次,然后在每次迭代过程中,比例因子也需要参与交换。
"伪代码与部分主元策略的差别如下:"

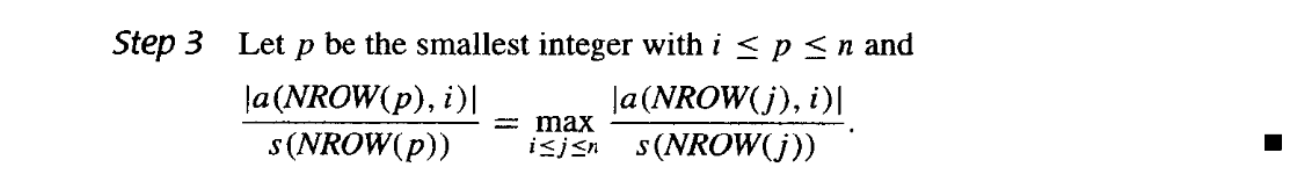
全主元选取策略 | Complete Pivoting
上个算法中,比例因子只在初始过程中计算一次。如果考虑到过程被修改,使得每次作行变换的决定时,要确定新的比例因子,那这种方法就是全主元选取策略(Complete Pivoting)。
6.5 矩阵分解 | Matrix Factorization
LU分解 | LU Factorization
假设Gauss消去法在此次解方程后没有进行行交换,Gauss消去法的第一步是对j=2,3,⋯,n行进行计算:
(Ej−mj1E1)→Ej,mj1=a11(1)aj1(1)
那我们可以把这个过程写成矩阵的形式:
1−m21−m31⋮−mn1010⋮0⋯⋯⋯⋱⋯000⋮1a11(1)a21(1)⋮an1(1)a12(1)a22(1)⋮an2(1)⋯⋯⋱⋯a1n(1)a2n(1)⋮ann(1)=a11(1)00⋮0a12(1)a22(2)a32(2)⋮an2(2)⋯⋯⋯⋱⋯a1n(1)a2n(2)a3n(2)⋮ann(2)
记最左边的矩阵为M(1),中间的矩阵为A(1),右边的矩阵为A(2),则有M(1)A(1)=A(2)。
这里的M(1)称作第一Gauss交换矩阵(first Gauss transformation matrix)。
用b(2)表示b(1)经过第一次Gauss消去法后的结果,则有A(2)x=M(1)A(1)x=M(1)b(1)=b(2)。
一般的,如果A(k)x=b(k)已经构建,则由第k个Gauss变换矩阵:
M(k)=10⋮000⋮001⋮⋯⋯⋯⋮⋯⋯0⋱⋯⋯⋯⋮⋯⋯⋯⋱1−mk+1,k−mk+2,k⋮−mn,k⋯⋯⋯010⋮0⋯⋯⋯⋯⋯⋱⋱⋯⋯⋯⋯⋯⋯⋯⋱⋯00⋮000⋮1
则有A(k+1)x=M(k)A(k)x=M(k)b(k)=b(k+1)。
这个过程结束在第A(n)x=b(n),这里的A(n)=M(n−1)A(n−2)=⋯=M(n−1)M(n−2)⋯M(1)A(1)。由高斯消元法知道,A(n)是一个上三角矩阵。
此过程就形成了A=LU的分解中的U部分,而L部分就是上文A左侧矩阵的逆矩阵,即(M(n−1)M(n−2)⋯M(1))−1=M(1)−1M(2)−1⋯M(n−1)−1。
因为M(k)的逆矩阵就是把对角线下方的元素取反,所以L的元素为:
L(k)=(M(k))−1=10⋮000⋮001⋮⋯⋯⋯⋮⋯⋯0⋱⋯⋯⋯⋮⋯⋯⋯⋱1mk+1,kmk+2,k⋮mn,k⋯⋯⋯010⋮0⋯⋯⋯⋯⋯⋱⋱⋯⋯⋯⋯⋯⋯⋯⋱⋯00⋮000⋮1
所以
L=L(1)L(2)⋯L(n−1)=1m21m31⋮mn101m32⋮mn2⋯0⋱⋱⋯⋯⋯⋱⋱mn,n−100⋮01
由此我们可以得到:
如果Gauss消去法在线性方程组Ax=b中没有进行行交换,则A=LU,
其中
L=L(1)L(2)⋯L(n−1)=1m21m31⋮mn101m32⋮mn2⋯0⋱⋱⋯⋯⋯⋱⋱mn,n−100⋮01
U=A(n)=a11(1)00⋮0a12(1)a22(2)0⋮0⋯⋯⋯⋱⋯a1n(1)a2n(2)a3n(3)⋮ann(n)
如果L是单位下三角矩阵,则这个分解是唯一的。
用反证法。
如果A=L1U1=L2U2,其中L1和L2是单位下三角矩阵,U1和U2是上三角矩阵。则有
U1U2−1=L1−1L2
因为上三角阵的逆依然是上三角阵,下三角阵同理。所以等式左右分别为上三角阵和下三角阵。又因为L1−1L2的对角线上的元素均为1,所以两式相等当且仅当
U1U2−1=L1−1L2=I
即U1=U2,L1=L2。
所以这个分解是唯一的。
伪代码
先进行LU分解。


解第一个方程Ly=b。

解第二个方程Ux=y。

6.6 特殊类型的矩阵 | Special Types of Matrices
严格对角占优矩阵 | Strictly Diagonally Dominant Matrices
如果对矩阵A的每一行,对角线上的元素的绝对值大于该行上其他元素的绝对值之和,则称A为严格对角占优矩阵。
定理:严格对角占优矩阵是非奇异的。而且,在此情况下,Gauss消去法可用在形如Ax=b的方程组中以得到唯一解,而且不需要进行或列交换,并且对于舍入误差的增长而言计算是稳定的。
正定矩阵 | Positive Definite Matrices
本书中的正定矩阵是指对称正定矩阵,与其他书中的定义不同。
一个矩阵A是正定的,如果它是对称的,并且对于所有非零向量x,都有xTAx>0。
"定理"
如果A是n×n的正定矩阵,则
a. A是非奇异的。
b. aii>0,i=1,2,⋯,n。
c. 1≤k,j≤nmax∣akj∣<1≤i≤nmax∣aii∣,其中 k=j。
d. (aij)2<aiiajj,i=j。
重要结论:如果A是正定的,则A的所有主子式都是正的。
A=LDLT分解
我们可以把A=LU中的U进一步分解为对角矩阵D和单位上三角矩阵U,如下图所示:
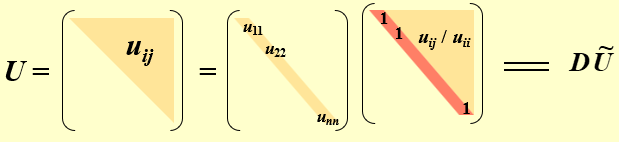
我们知道,A是对称的,所以A=AT,即LU=LDU=UTDLT,所以可以有L=UT,所以A=LDLT。其中L是一个主对角线为1的下三角矩阵,D是对角线元素为正值的对角矩阵。
伪代码如下:

Cholesky分解
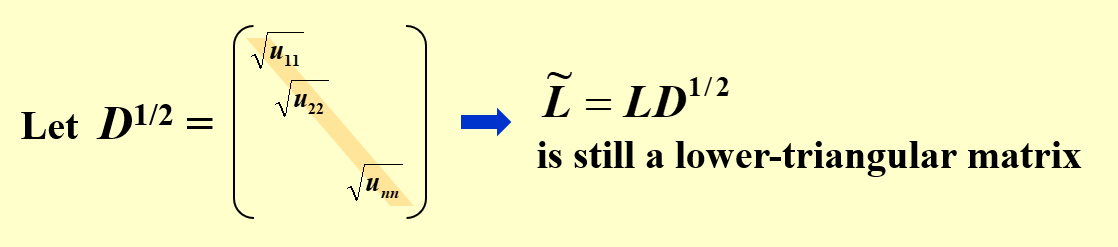
取L=LD21,则有A=LLT。其中L是一个具有非零对角线元素的下三角矩阵。
伪代码如下:
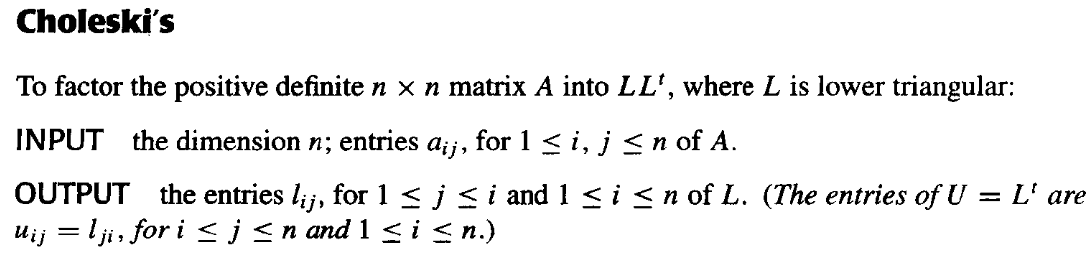
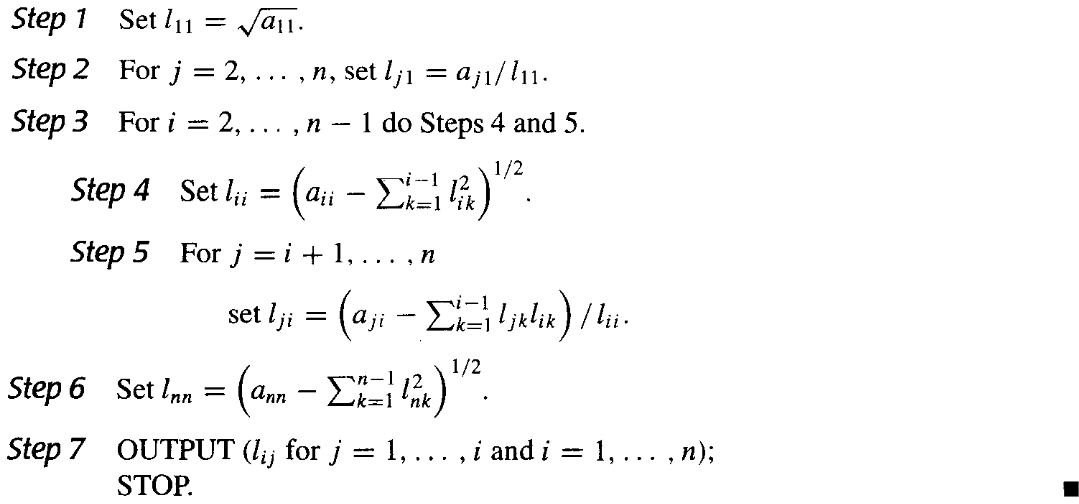
三对角矩阵 | Tridiagonal Matrices
三对角矩阵是指除了对角线和对角线上方和下方的第一条对角线外,其他元素均为0的矩阵,形式如下:
a11a210⋮⋮0a12a22a32⋱⋯⋯0a23a33⋱⋱⋯⋯0a34⋱⋱0⋯⋯⋯⋱⋱an,n−1000⋮an−1,nann
定理:假设A是三对角矩阵,对每个i=2,3,⋯,n−1,有ai,i−1ai,i+1=0,如果∣a11∣>∣a12∣,∣aii∣>∣ai,i−1∣+∣ai,i+1∣,∣ann∣>∣an,n−1∣,则A是非奇异的,且在Crout分解中,lii的值都是非零的。
Crout分解
Crout分解是LU分解的一种特殊情况,我们可以求出具有形式
L=l11l210⋮00l22l32⋱⋯00l33⋱0⋯⋯⋯⋱ln,n−1000⋮lnn,U=100⋮0u1210⋱⋯0u231⋱0⋯⋯⋯⋱0000⋮1
的三对角矩阵A的分解。
通过矩阵乘法,我们可以得到:
⎩⎨⎧a11=l11ai,i−1=li,i−1ai,i=li,i−1ui−1,i+li,iai,i+1=li,iui,i+1
在求解部分,我们可以先解Lz=b,然后再解Ux=z。有伪代码:

Chapter 7 矩阵代数中的迭代方法 | Iterative Techniques in Matrix Algebra
7.1 向量和矩阵范数 | Norms of Vectors and Matrices
向量范数
Rn上的向量范数是一个函数∥⋅∥:Rn→R,满足下列条件:
- ∥x∥≥0,且∥x∥=0当且仅当x=0;(x∈Rn)
- ∥αx∥=∣α∣∥x∥,其中α∈R,x∈Rn;
- ∥x+y∥≤∥x∥+∥y∥。(x,y∈Rn)
常用的向量范数有:
- p-范数:∥x∥p=(i=1∑n∣xi∣p)1/p,其中p≥1;
- 无穷范数:∥x∥∞=max1≤i≤n∣xi∣;
向量的收敛性
Rn上的向量序列{x(k)}k=1∞按照向量范数∥⋅∥收敛到向量x,当且仅当对于任意的ϵ>0,存在整数N(ϵ),使得当k>N(ϵ)时,有∥x(k)−x∥<ϵ。
对于无穷范数,如果向量序列{x(k)}k=1∞按照无穷范数∥⋅∥∞收敛到向量x,当且仅当对于任意i=1,2,⋯,n,有limk→∞xi(k)=xi。
范数的等价性
等价性定义:Rn上的向量范数∥⋅∥和∥⋅∥′等价,当且仅当存在正常数c1,c2,使得对于任意的x∈Rn,有c1∥x∥≤∥x∥′≤c2∥x∥。
实际上,Rn上的所有范数都是等价的。也就是说,如果∥⋅∥和∥⋅∥′是Rn上的任意两个范数,并且{x(k)}k=1∞按照∥⋅∥收敛到x,那么{x(k)}k=1∞也按照∥⋅∥′收敛到x。
我们接下来证明对于范数∥⋅∥2和∥⋅∥∞,它们是等价的。
"∥⋅∥2和∥⋅∥∞的等价性"
设∥x∥∞=1≤i≤nmax∣xi∣=∣xj∣。那么
∥x∥2=i=1∑n∣xi∣2≥∣xj∣2=∣xj∣=∥x∥∞
并且
∥x∥2=i=1∑n∣xi∣2≤i=1∑n∣xj∣2=n∣xj∣
所以∥x∥∞≤∥x∥2≤n∥x∥∞,即∥⋅∥2和∥⋅∥∞是等价的。
矩阵范数
Rn×n上的矩阵范数是一个函数∥⋅∥:Rn×n→R,满足下列条件:
- ∥A∥≥0,且∥A∥=0当且仅当A是零矩阵;(A∈Rn×n)
- ∥αA∥=∣α∣∥A∥,其中α∈R,A∈Rn×n;
- ∥A+B∥≤∥A∥+∥B∥。(A,B∈Rn×n)
- ∥AB∥≤∥A∥∥B∥。(A,B∈Rn×n)
矩阵A和B之间的距离定义为∥A−B∥。
Frobenius范数
A∈Rn×n的Frobenius范数是A的所有元素的平方和的平方根,即∥A∥F=i=1∑nj=1∑naij2。
自然矩阵范数 | Natural Matrix Norm
如果∥⋅∥是Rn×n上的向量范数,那么∥A∥=∥x∥=1max∥Ax∥是Rn×n上的矩阵范数,称为与向量范数∥⋅∥相关的自然矩阵范数。
∥A∥=∥x∥=1max∥Ax∥也可以写成∥A∥=x=0max∥x∥∥Ax∥。
常用的自然矩阵范数(Natural Norm)有:
- p-范数:∥A∥p=x=0max∥x∥p∥Ax∥p,其中p≥1;
- 无穷范数:∥A∥∞=1≤i≤nmaxj=1∑n∣aij∣;也就是A的所有行和的最大值;
- 1-范数:∥A∥1=1≤j≤nmaxi=1∑n∣aij∣;也就是A的所有列和的最大值;
- 2-范数(spectral norm):∥A∥2=λmax(ATA),其中λmax(ATA)是ATA的最大特征值。
"推论"
根据 p-范数的定义,我们可以得到:对于任意非零向量 z 和矩阵 A 和任意一个自然范数 ∥⋅∥,有
∥z∥∥Az∥≤∥A∥
即
∥Az∥≤∥A∥∥z∥
7.2 特征值与特征向量 | Eigenvalues and Eigenvectors
谱半径 | Spectral Radius
A∈Rn×n的谱半径定义为ρ(A)=1≤i≤nmax∣λi∣,其中λi是A的特征值,这里的特征值可以是复数。
ρ(A)=max{1,∣1+3i∣,∣1−3i∣}=max{1,2,2}=2。
对于任意一个自然范数∥⋅∥,有ρ(A)≤∥A∥。
矩阵的收敛性
当满足以下条件时,矩阵A∈Rn×n是收敛的:
k→∞lim(Ak)ij=0
以下命题是等价的:
- 矩阵A∈Rn×n是收敛的;
- ρ(A)<1;
- 对于某些自然范数∥⋅∥,有k→∞lim∥Ak∥=0。
- 对于任意的自然范数∥⋅∥,有k→∞lim∥Ak∥=0。
- 对于每一个x∈Rn,有k→∞limAkx=0。
7.3 求解线性方程组的迭代法 | Iterative Techniques for Solving Linear Systems
Jacobi迭代法
记矩阵A∈Rn×n的下三角部分为−L,上三角部分为−U,对角线部分为D,即A=D−L−U。
所以方程组Ax=b可以写成Dx=(L+U)x+b。
即x=D−1(L+U)x+D−1b。
引入符号Tj=D−1(L+U),cj=D−1b,则x=Tjx+cj。
Jacobi迭代法的迭代格式为:
x(k+1)=Tjx(k)+cj
其伪代码为:

Gauss-Seidel迭代法
我们可以改进Jacobi迭代法,使得每次迭代时,都使用已经算出来的x(k)的元素来计算x(k)之后的元素。如下图所示:

也就是说,可以使用:
xi(k)=aii−j=1∑i−1aijxj(k)−j=i+1∑naijxj(k−1)+bi
来计算xi(k)。
结合之前D,L,U的定义,我们可以得到:
(D−L)x(k)=Ux(k−1)+b
即:
x(k)=(D−L)−1Ux(k−1)+(D−L)−1b
引入符号Tg=(D−L)−1U,cg=(D−L)−1b,则x=Tgx(k−1)+cg。
Gauss-Seidel迭代法的迭代格式为:
x(k+1)=Tgx(k)+cg
其伪代码为:


两种迭代法的收敛性
对于任意一个x(0)∈Rn,由
x(k+1)=Tx(k)+c
定义的序列 {x(k)}k=0∞ 收敛到x=Tx+c的唯一解,当且仅当ρ(T)<1。
"证明"
⇐:
设ρ(T)<1,那么
x(k)===⋮=Tx(k−1)+cT(Tx(k−2)+c)+cT2x(k−2)+(T+I)cTkx(0)+(Tk−1+Tk−2+⋯+T+I)c
由于ρ(T)<1,所以矩阵T是收敛的,且k→∞limTkx(0)=0
由于k→∞lim(Tk−1+Tk−2+⋯+T+I)c=(I−T)−1c,所以k→∞limx(k)=(I−T)−1c=x,这里的x就是x=Tx+c的唯一解。
⇒:
设{x(k)}k=0∞收敛到x=Tx+c的唯一解,取任意一个向量y∈Rn,定义x(0)=x−y,那么
x−x(k)=(Tx+c)−(Tx(k−1)+c)=T(x−x(k−1))
所以
x−x(k)=Tk(x−x(0))=Tky
因此
k→∞limTky=k→∞lim(x−x(k))=0
由于y是任意的,根据矩阵的收敛性,ρ(T)<1。
误差界 | Error Bounds for Iterative Methods
如果对任意自然矩阵范数∥T∥<1,c是给定的向量,那么由x(k+1)=Tx(k)+c定义的序列{x(k)}k=0∞收敛到x=Tx+c的唯一解,且有误差界:
- ∥x−x(k)∥≤∥T∥k∥x(0)−x∥;
- ∥x−x(k)∥≤1−∥T∥∥T∥k∥x(1)−x(0)∥;
通过(2)式,我们可以根据我们要的精度算出迭代次数k
"证明(1)式"
x−x(k)=(Tx+c)−(Tx(k−1)+c)=T(x−x(k−1))
所以
∥x−x(k)∥=∥T(x−x(k−1))∥≤∥T∥∥x−x(k−1)∥≤∥T∥k∥x−x(0)∥
∥x(k)−x∥≈ρ(T)k∥x(0)−x∥
"证明(2)式"
∥x(k+1)−x(k)∥=∥T(x(k)−x(k−1))∥≤∥T∥∥x(k)−x(k−1)∥≤∥T∥k∥x(1)−x(0)∥
所以对于任意的m≥n,有
∥x(m)−x(n)∥=∥x(m)−x(m−1)+x(m−1)−x(m−2)+⋯+x(n+1)−x(n)∥≤∥x(m)−x(m−1)∥+∥x(m−1)−x(m−2)∥+⋯+∥x(n+1)−x(n)∥≤∥T∥m−1∥x(1)−x(0)∥+∥T∥m−2∥x(1)−x(0)∥+⋯+∥T∥n∥x(1)−x(0)∥=∥x(1)−x(0)∥k=n∑m−1∥T∥k
当m→∞时,k=n∑m−1∥T∥k=1−∥T∥∥T∥n,所以
∥x−x(n)∥≤1−∥T∥∥T∥n∥x(1)−x(0)∥
对于严格对角占优矩阵
如果A是严格对角占优的,那么Jacobi迭代法和Gauss-Seidel迭代法都是收敛的。
松弛法 | Relaxation Methods
假设x~∈Rn是Ax=b的一个近似解,那么相对于该方程组的剩余向量(residual vector)为r=b−Ax~。
我们从剩余向量的视角来看Gauss-Seidel迭代法。
xi(k)=aii−j=1∑i−1aijxj(k)−j=i+1∑naijxj(k−1)+bi=xi(k−1)+aii1(bi−j=1∑i−1aijxj(k)−j=i∑naijxj(k−1))=xi(k−1)+aiiri(k)
我们可以添加一个参数ω,使得
xi(k)=xi(k−1)+ωaiiri(k)
这就是松弛法的基本思想,可以用来减少剩余向量的范数和加速收敛。
根据ω的取值,松弛法可以分为:
- ω<1:欠松弛法(Under-Relaxation methods);可使由Gauss-Seidel方法不能收敛的方程组收敛;
- ω=1:退化为Gauss-Seidel迭代法;
- ω>1:超松弛法(Over-Relaxation methods);可使收敛速度加快。
这些方法缩写为SOR方法(Successive Over-Relaxation)。
SOR方法的矩阵形式
我们尝试把SOR方法的迭代格式写成矩阵形式:
xi(k)=xi(k−1)+ωaiiri(k)=xi(k−1)+aiiω(bi−j=1∑i−1aijxj(k)−j=i∑naijxj(k−1))=(1−ω)xi(k−1)+aiiω(bi−j=1∑i−1aijxj(k)−j=i+1∑naijxj(k−1))
所以
x(k)(I−ωD−1L)x(k)x(k)x(k)=(1−ω)x(k−1)+ωD−1(b+Lx(k)+Ux(k−1))=((1−ω)I+ωD−1U)x(k−1)+ωD−1b=(I−ωD−1L)−1((1−ω)I+ωD−1U)x(k−1)+(I−ωD−1L)−1ωD−1b=(D−ωL)−1((1−ω)D+ωU)x(k−1)+ω(D−ωL)−1b
记Tω=(D−ωL)−1((1−ω)D+ωU),cω=ω(D−ωL)−1b,则SOR方法的迭代格式为:
x(k)=Tωx(k−1)+cω
Kahan定理
如果aii=0(i=1,2,⋯,n),那么ρ(Tω)≥∣ω−1∣。这表明,SOR方法当且仅当ω∈(0,2)时收敛。
Ostrowski-Reich定理
如果A是一个正定矩阵,并且ω∈(0,2),那么SOR方法对于任意的初始近似向量x(0)∈Rn都收敛。
ω的最佳选择
如果A是一个正定的三对角矩阵,那么ρ(Tg)=[ρ(Tj)]2<1,并且SOR方法的最佳ω选择是:
ωopt=1+1−[ρ(Tj)]22
由此选择的ω,有ρ(Tω)=ω−1。
SOR伪代码

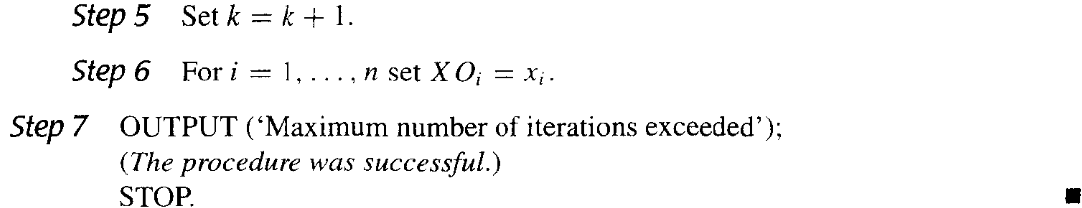
7.4 误差界与迭代改进 | Error Bounds and Iterative Refinement
误差界
对于线性方程组 Ax=b ,A是非奇异的。如果 A 和 b 存在误差,那么解 x 也会存在误差。
A 精确,b 有误差
即 Ax=b 变成 A(x+δx)=b+δb 。所以有:
Aδx⇒δx=δb=A−1δb
根据推论
对于任意向量 z=0,矩阵 A 和任意一个自然范数 ∥⋅∥,有
∥z∥∥Az∥≤∥A∥
我们有:
∥δx∥≤∥A−1∥∥δb∥
b=Ax⇒∥b∥=∥Ax∥≤∥A∥∥x∥
所以
∥x∥∥δx∥≤∥A∥∥A−1∥∥b∥∥δb∥
我们记非奇异矩阵 A 相对于范数 ∥⋅∥ 的条件数为:
K(A)=∥A∥∥A−1∥
当 K(A) 很大时,A 是病态的,当 K(A) 接近于 1 时,A 是良态的。
A 有误差,b 精确
即 Ax=b 变成 (A+δA)(x+δx)=b 。所以有:
(A+δA)δx+xδA=0
这里的 δA 往往是一个小量。
"证明∥(I+A−1δA)−1∥≤1−∥A−1δA∥1"
"推论"
对于矩阵 F,若∥F∥<1,则I±F是非奇异的,且
(I±F)−1≤1−∥F∥1
"下面给出 I−F情况的证明"
因为 ∥−F∥=∥F∥<1,所以我们将−F替换 F ,就可以得到 I+F情况的证明

"推论"
∥A−1∥p=min∣∣x∣∣p∣∣Ax∣∣p1
"证明"
=====∥A−1∥px=0max∥x∥p∥A−1x∥p)Ax=0max∥A−1x∥p∥A−1Ax∥px=0max∥Ax∥p∥x∥px=0max∥x∥p∥Ax∥p1min∣∣x∣∣p∣∣Ax∣∣p1
我们有
(A+δA)=A(I+A−1δA)
而
∥A−1δA∥≤∥A−1∥∥δA∥=min∣∣x1∣∣p∣∣Ax1∣∣p∥δA∥
因为∥δA∥相对于∥A∥很小,所以往往有∥A−1δA∥≤1,所以I+A−1δA是非奇异的,且
∥(I+A−1δA)−1∥≤1−∥A−1δA∥1
所以在∥A−1δA∥≤1的情况下(我们不妨将其放缩为∥δA∥≤∥A−11∥),有:
∥(I+A−1δA)−1∥≤1−∥A−1δA∥1
所以
(A+δA)δx+xδAA(I+A−1δA)δxδx∥δx∥=0=−xδA=−(I+A−1δA)−1A−1xδA≤∥(I+A−1δA)−1∥∥A−1∥∥x∥∥δA∥≤1−∥A−1∥∥δA∥∥A−1∥∥x∥∥δA∥
所以:
∥x∥∥δx∥≤1−∥A−1∥∥δA∥∥A−1∥∥δA∥=1−K(A)∥A∥∥δA∥K(A)∥A∥∥δA∥
A,b 都有误差
即 Ax=b 变成 (A+δA)(x+δx)=b+δb 。所以有:
(A+δA)δx+xδA=δb
所以,当∥δA∥<∥A−1∥1时,有:
δx=(I+A−1δA)−1A−1(δb−xδA)
所以
∥δx∥≤1−∥A−1∥∥δA∥∥A−1∥∥δb−xδA∥≤1−∥A−1∥∥δA∥∥A−1∥(∥δb∥+∥x∥∥δA∥)≤1−K(A)∥A∥∥δA∥K(A)(∥A∥∥δb∥+∥A∥∥x∥∥δA∥)≤1−K(A)∥A∥∥δA∥K(A)(∥A∥∥x∥∥δb∥+∥A∥∥δA∥)∥x∥≤1−K(A)∥A∥∥δA∥K(A)(∥Ax∥∥δb∥+∥A∥∥δA∥)∥x∥≤1−K(A)∥A∥∥δA∥K(A)(∥b∥∥δb∥+∥A∥∥δA∥)∥x∥
因此,当∥δA∥<∥A−1∥1时,有:
∥x∥∥δx∥≤1−K(A)∥A∥∥δA∥K(A)(∥b∥∥δb∥+∥A∥∥δA∥)
K(A) 的性质
我们记非奇异矩阵 A 相对于范数 ∥⋅∥ 的条件数为:
K(A)=∥A∥∥A−1∥
当 K(A) 很大时,A 是病态的,当 K(A) 接近于 1 时,A 是良态的。
- K(A)p≥1 对所有的自然范数 ∥⋅∥p 成立;
- 如果 A 是对称的,那么 K(A)2=∣λmin∣∣λmax∣,其中 λmax 和 λmin 分别是 A 的最大和最小特征值;
- K(aA)=K(A),其中 a 是一个非零常数;
- K(A)2=1 当且仅当 A 是正交矩阵(ATA=I);
- K(RA)2=K(AR)2=K(A)2,其中 R 是一个正交矩阵;
题目例子
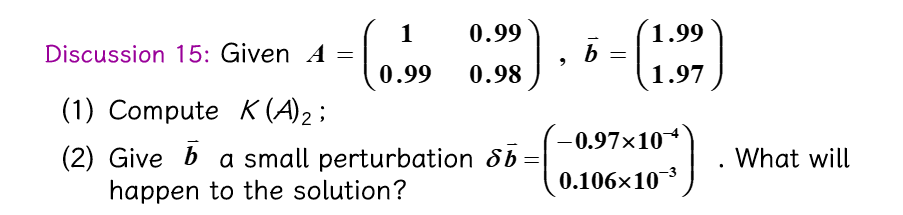
"(1)"
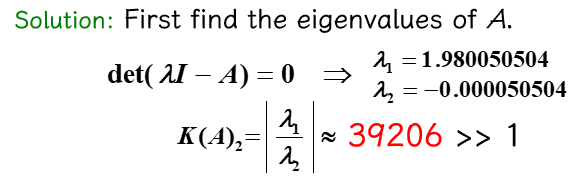
"(2)"
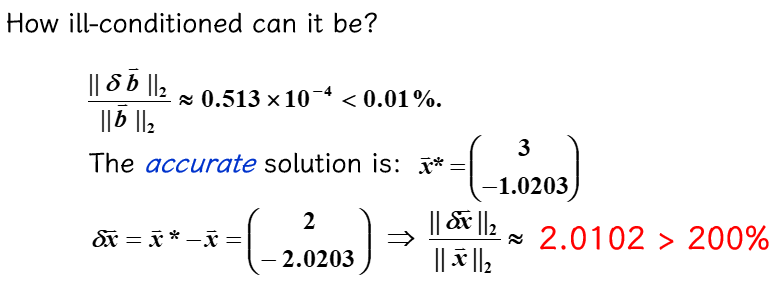
Chapter 8 逼近论 | Approximation Theory
逼近和插值的区别在于,插值是要求通过所有的数据点,而逼近没有这个限制,而是要求逼近的函数和原函数的误差尽可能小——尽可能接近每个点。
8.1 Discrete Least Squares Approximation | 离散最小二乘逼近
误差表达
设 p(x) 是逼近函数,yi 是给定的 n 个数据点,那么逼近误差的三种表达方式如下:
Minimax problem
E∞(p)=max{∣yi−f(x)∣}
这用初等技术是解决不了的
Absolute deviation
E1(p)=i=1∑n∣yi−f(x)∣
困难在于绝对值函数在零点不可微,可能无法求解多元函数的最小值。
Least squares
E2(p)=i=1∑n(yi−f(x))2
此即为最小二乘的误差表达,也是最常用的逼近方法。
我们的目标是找到一个 p(x),使得 E2(p) 最小。
离散最小二乘逼近
定义: Pn(x) 是 m 个数据点的离散最小二乘逼近,如果 Pn(x) 是 n 次多项式,且满足
p=argp∈Pnmini=1∑m(yi−p(xi))2
其中 Pn 是 n 次多项式的集合,n 应远远小于 m,如果 n=m−1,其即为 lagrange 插值。
离散最小二乘逼近的解
设 Pn(x)=a0+a1x+⋯+anxn=i=0∑naixi。
E2=i=1∑m(yi−Pn(xi))2
为了使 E2 最小,则其必要条件是
∂ak∂E2=0,k=0,1,⋯,n
即
∂ak∂E2=2i=1∑m(Pn(xi)−yi)∂ak∂Pn(xi)=2i=1∑m(j=0∑najxij−yi)xik=2(j=0∑n(aji=1∑mxij+k)−i=1∑myixik)=0
即
j=0∑n(aji=1∑mxij+k)=i=1∑myixik,k=0,1,⋯,n
也就是
i=1∑mxi0i=1∑mxi1⋮i=1∑mxini=1∑mxi1i=1∑mxi2⋮i=1∑mxin+1⋯⋯⋱⋯i=1∑mxini=1∑mxin+1⋮i=1∑mxi2na0a1⋮an=i=1∑myixi0i=1∑myixi1⋮i=1∑myixin
P(x) 线性
即 n=1 。此时,P1(x)=a0+a1x,有
mi=1∑mxii=1∑mxii=1∑mxi2[a0a1]=i=1∑myii=1∑myixi
所以
⎩⎨⎧a0=mi=1∑mxi2−(i=1∑mxi)2i=1∑mxi2i=1∑myi−i=1∑mxii=1∑mxiyia1=mi=1∑mxi2−(i=1∑mxi)2mi=1∑mxiyi−i=1∑mxii=1∑myi
P(x)=ax+bx
令 Yi=yi1,Xi=xi1,则可化为
Yi=a+bXi
线性最小二乘即可
P(x)=ae−b/x
令 Yi=lnyi,Xi=xi1,则可化为
Yi=lna−bXi
线性最小二乘即可。
8.2 Orthogonal Polynomials and Least Squares Approximation | 正交多项式与最小二乘逼近
刚刚是离散化的最小二乘逼近,现在是连续的最小二乘逼近。
给定定义在 [a,b] 上的函数 f(x),我们希望找到一个 简单的函数 p(x) 来逼近 f(x),使得
E=∫ab∣f(x)−p(x)∣2dx
最小。
广义多项式(Generalized Polynomial):用线性无关的函数 ϕ0(x),ϕ1(x),⋯,ϕn(x) 的线性组合 P(x)=i=0∑naiϕi(x) 来逼近 f(x),这里的 P(x) 称为广义多项式。
- Trigonometric polynomial: ϕi(x)=cos(ix) or sin(ix)
- Exponential polynomial: ϕi(x)=ekix,ki=kj
- 记 Πn(x) 为 阶数最多为 n 的多项式的集合,Πn(x) 是一个线性空间,Πn(x) 的基为 {1,x,x2,⋯,xn},可以拿来做广义多项式的基。
Weight Function | 权函数
离散的情况下,为了在某些点上分配不同程度的重要性,我们在计算离散最小二乘逼近的误差表达式时附上权重:
E=i=1∑mwi(yi−p(xi))2
连续的情况下,我们也可以引入权重函数 w(x),使得
E=∫abw(x)∣f(x)−p(x)∣2dx
Inner Product and Norm | 内积与范数
我们定义内积为
⟨f,g⟩=⎩⎨⎧i=1∑mwif(xi)g(xi)∫abw(x)f(x)g(x)dx离散连续
如果 ⟨f,g⟩=0,则称 f 和 g 正交。
我们定义范数为
∥f∥=⟨f,f⟩
所以我们可以把误差表达式写成
E=⟨f−p,f−p⟩=∥f−p∥2
寻找多项式的系数
设 P(x)=a0ϕ0(x)+a1ϕ1(x)+⋯+anϕn(x),与离散的情况类似,我们要使得 E 最小,即
∂ak∂E∂ak∂(∫abw(x)i=0∑naiϕi(x)−f(x)2)dx∂ak∂(∫abw(x)((i=0∑naiϕi(x))2−2f(x)i=0∑naiϕi(x)+f(x)2))dx∫abw(x)(2ϕk(x)i=0∑naiϕi(x)−2f(x)ϕk(x))dx∫abw(x)ϕk(x)i=0∑naiϕi(x)dxi=0∑nai∫abw(x)ϕk(x)ϕi(x)dxi=0∑nai⟨ϕk,ϕi⟩=0=0=0=0=∫abw(x)ϕk(x)f(x)dx=∫abw(x)ϕk(x)f(x)dx=⟨ϕk,f⟩
写成矩阵形式即为
⟨ϕ0,ϕ0⟩⟨ϕ1,ϕ0⟩⋮⟨ϕn,ϕ0⟩⟨ϕ0,ϕ1⟩⟨ϕ1,ϕ1⟩⋮⟨ϕn,ϕ1⟩⋯⋯⋱⋯⟨ϕ0,ϕn⟩⟨ϕ1,ϕn⟩⋮⟨ϕn,ϕn⟩a0a1⋮an=⟨ϕ0,f⟩⟨ϕ1,f⟩⋮⟨ϕn,f⟩
"离散例子"
可以证明,离散时的式子也是这样的。

构造正交多项式
由 Hij(n)=i+j−11 定义的 n×n 的 Hilbert 矩阵是一个病态矩阵。在求解中往往因为舍入误差而导致结果不准确。
为了解决这个问题,我们可以通过正交化的方法来构造正交多项式,也就是让前文中提到的矩阵变成对角矩阵。这样就不需要进行求逆了。
此时的系数可以直接通过
ak=⟨ϕk,ϕk⟩⟨ϕk,f⟩
来计算。
我们可以构造出一系列的正交多项式。用下面定义的多项式函数集 {ϕ0(x),ϕ1(x),⋯,ϕn(x)} 关于权函数 w(x) 是正交的:
ϕ0(x)=1,ϕ1(x)=x−B1,ϕk(x)=(x−Bk)ϕk−1(x)−Ckϕk−2(x),k=2,3,⋯
其中 Bk 和 Ck 是常数,可以通过
Bk=⟨ϕk−1,ϕk−1⟩⟨xϕk−1,ϕk−1⟩,Ck=⟨ϕk−2,ϕk−2⟩⟨xϕk−1,ϕk−2⟩
来计算。
"题目例子"

里面各项已经在之前的图片中计算过了。
伪代码

其中误差的计算推导如下:
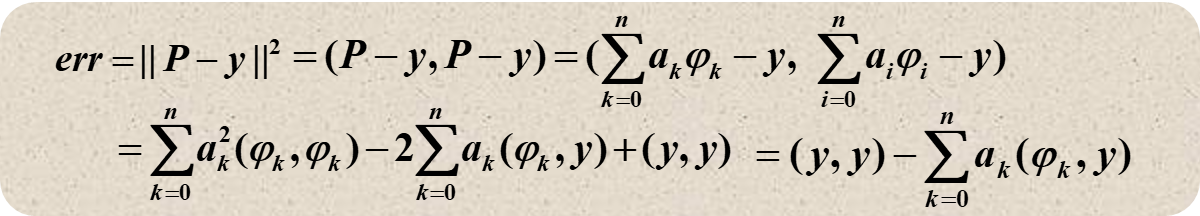
8.3 Chebyshev Polynomials and Economization of Power Series | 切比雪夫多项式与幂级数的缩减
Chebyshev Polynomials | 切比雪夫多项式
Target 1
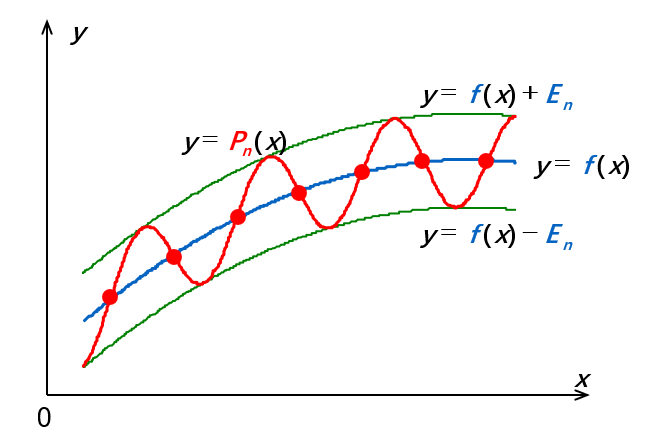
上文我们知道了误差的计算方式,现在我们试图找到一个 n 阶多项式 Pn 来逼近函数,使得误差 ∥Pn−f∥ 最小。
若 P(x0)−f(x0)=±∥Pn−f∥ ,则定义点 x0 为 Deviation point
我们的多项式 Pn 有如下性质:
-
如果 f∈C[a,b],且 f 不是 n 阶多项式,则存在唯一的多项式 Pn 使得 ∣∣Pn−f∣∣∞ 最小
-
Pn(x) 存在,且必须有正负偏差点,否则肯定还有更好的逼近函数
-
(切比雪夫定理)Pn(x) 最小化 ∣∣Pn−f∣∣∞ ⇔ Pn(x) 至少有 n+2 个正负偏差点。也就是说,存在一组点 a≤t1<⋯<tn+2≤b,使得
Pn(tk)−f(tk)=±(−1)k∣∣Pn−f∣∣∞
这组点 {tk} 被称为切比雪夫交替序列(Chebyshev alternating sequence)。
Target 2.0
决定插值点 {x0,⋯,xn} 使得 Pn(x) 最小化余项。余项为:
∣Pn(x)−f(x)∣=∣Rn(x)∣=(n+1)!f(n+1)(ξ)i=0∏n(x−xi)
Target 2.1
找到插值点 {x1,⋯,xn} 使得 ∣∣wn∣∣∞ 在 [−1,1]上最小化,其中 wn(x)=i=1∏n(x−xi)
注意到
wn(x)=xn−Pn−1(x)
这里的 Pn−1(x) 是 n−1 阶多项式,和上文的 Pn(x) 不是一个东西,此语境下没有关联。
Target 3.0
问题转化为找到 x1,⋯,xn 使得 ∣∣xn−Pn−1(x)∣∣∞ 在 [−1,1]上最小化。
从切比雪夫定理我们知道,Pn−1(x) 相对于 xn 有 n+1 个偏差点,也就是说,wn(x) 在 n+1 个点上交替取得最大值和最小值。
引入Chebyshev Polynomials
为了实现上面的目标,我们先想到三角函数。cos(nθ) 在 [−1,1] 上有 n+1 个交替的最大值和最小值,但是 cos(nθ) 不是多项式。
又由于 cos(nθ) 可以表示为 k=0∑nak(cosθ)k,这就是我们想要的多项式形式。
令 x=cosθ,则 x∈[−1,1],所以我们可以把 cos(nθ) 写成 Tn(x) 的形式,Tn(x) 称为切比雪夫多项式(Chebyshev polynomial)。
Tn(x)=cos(n⋅arccosx)
切比雪夫多项式的性质:
- 当 x=cosnkπ 时,Tn(x) 取到极值 (−1)k
我们也可以用递推公式来定义切比雪夫多项式:
T0(x)T1(x)Tn(x)=1=x=2xTn−1(x)−Tn−2(x),n=2,3,⋯
可以得出性质:
- 最高阶项的系数为 2n−1
- 在[0,1]上,T0(x),T1(x),⋯,Tn(x) 关于权函数 1−x21 正交
通过计算得出
⟨Tn,Tm⟩=∫−111−x2Tn(x)Tm(x)dx=⎩⎨⎧π2π0n=m=0n=m=0n=m
回到 Target 3.0
我们可以把 wn 写成 Tn(x) 的形式:
wn(x)=xn−Pn−1(x)=2n−1Tn(x)
称之为首一切比雪夫多项式(The monic Chebyshev polynomial)。
可以证明,首一切比雪夫多项式是所有首一多项式中,最小化 ∣∣wn∣∣∞ 的多项式。
回到 Target 2.1
我们将 wn 写成 Tn(x) 的形式:
wn∈Π~nmin∥wn∥∞=2n−1Tn(x)∞=2n−11
这里的 Π~n 是所有首一多项式的集合。
所以,我们取的插值点即为 Tn(x) 的 n 个零点
回到 Target 2.0
在 [−1,1]上选取的插值点为T_n(x)的n$ 个零点,能够使得余项最小,其上确界为
x∈[−1,1]max∣f(x)−Pn(x)∣≤2n(n+1)!1x∈[−1,1]maxf(n+1)(x)
使用线性变换 x=2b−at+2b+a,我们可以将其推广到闭区间 [a,b] 上。
例题

Economization of Power Series | 幂级数的缩减
考虑到,用一个 n 阶多项式 Pn(x)=anxn+an−1xn−1+⋯+a1x+a0 来逼近一个任意的 n 阶多项式 Pn(x),我们可以通过去掉 Pn(x) 中的 含 anxn 项的 n 阶多项式 Qn(x) 来逼近 Pn(x),那么
x∈[−1,1]max∣f(x)−Pn−1(x)∣≤x∈[−1,1]max∣f(x)−Pn(x)∣+x∈[−1,1]max∣Qn(x)∣+x∈[−1,1]max∣Pn(x)−Pn−1(x)−Qn(x)∣≤x∈[−1,1]max∣f(x)−Pn(x)∣+x∈[−1,1]max∣Qn(x)∣
为了使得精确度的损失最小, Qn(x) 必须为
an⋅2n−1Tn(x)
例题

Chapter 9 逼近特征值 | Approximating Eigenvalues
9.2 幂法 | Power Method
幂法是用来确定矩阵的主特征值(即,绝对值最大的特征值)和对应的特征向量的一种方法。
基本思想
设A是一个n×n的矩阵,且恰有一个特征值λ1的绝对值最大
有n个特征值λ1,λ2,⋯,λn(∣λ1∣>∣λ2∣≥⋯≥∣λn∣),对应的特征向量为v1,v2,⋯,vn,则任意一个非零向量x(0)都可以表示为这n个特征向量的线性组合,记βj为常数,则
x(0)=j=1∑nβjvj
x(0)=0,且(x(0),v1)=0,否则:因为我们无法确保对于任意的初始向量x(0)都有β1=0,所以迭代的结果可能不是v1,而是满足 (x(0),vm)=0 的第一个向量vm,相应地,得到的特征值为 λm 。
等式两边同时左乘A,A2,⋯,Ak,得到
x(1)=Axx(2)=A2xx(k)=Akx=j=1∑nβjAvj=j=1∑nβjλjvj=j=1∑nβjA2vj=j=1∑nβjλj2vj⋮=j=1∑nβjAkvj=j=1∑nβjλjkvj=λ1kj=1∑nβj(λ1λj)kvj
所以
k→∞limAkx=k→∞limλ1kj=1∑nβj(λ1λj)kvj=k→∞limβ1λ1kv1
如果∣λ1∣<1,则k→∞limAkx=0,即x收敛到0向量。如果∣λ1∣>1,则序列发散。
对足够大的k,x(k),x(k−1)可以近似地表示为
x(k)≈β1λ1kv1,x(k−1)≈β1λ1k−1v1⇒x(k−1)x(k)≈λ1
所以,我们可以通过迭代x(k)=Ax(k−1)来逼近λ1。
归一化
实际计算时,为了避免计算过程中出现绝对值过大或过小的数参加运算,通常在每步迭代时,将向量“归一化”即用的按模最大的分量。
我们需要对x(k)进行归一化,使得∥x(k)∥∞=1,即
u(k−1)=∥x(k−1)∥∞x(k−1),x(k)=Au(k−1)⇒u(k)=∥x(k)∥∞x(k),λ1≈ui(k−1)xi(k)=∥x(k)∥∞
伪代码


- 对唯一的主特征值λ1,如果其重数大于1,则幂法仍然有效
- 如果λ1=−λ2,则幂法失效
- 因为我们无法确保对于任意的初始向量x(0)都有β1=0,所以迭代的结果可能不是v1,而是满足 (x(0),vm)=0 的第一个向量vm,相应地,得到的特征值为 λm 。
- Aitken's Δ2 可以加速收敛
收敛速度
因为x(k)=λ1kj=1∑nβj(λ1λj)kvj,假设λ1>λ2≥⋯≥λn,且∣λ2∣≥∣λn∣,则我们的目标就是让λ1λ2尽可能小,这样收敛速度更快。

记B=A−pI,其中p=2λ2+λn,则B的特征值为λ1−p,λ2−p,⋯,λn−p,因为∣λ1−pλ2−p∣<∣λ1λ2∣,所以此时B的收敛速度更快。
但是我们并不知道λ2和λn,所以这不一定是一个好的选择。
反幂法 | Inverse Power Method
反幂法一般是用来确定A中与特定数q最接近的特征值,即λi≈q。
此时对任意的j=i,有
∣λi−q∣≪∣λj−q∣
根据刚刚在收敛速度中的分析,可知:此时 (A−qI)−1 的主特征值凸显出来了,可以更快地收敛到 λi−q1。
其伪代码为: